Abstract
Objective
The aim of this study was to generate synthetic electronic health records (EHRs). The generated EHR data will be more realistic than those generated using the existing medical Generative Adversarial Network (medGAN) method.
Materials and Methods
We modified medGAN to obtain two synthetic data generation models—designated as medical Wasserstein GAN with gradient penalty (medWGAN) and medical boundary-seeking GAN (medBGAN)—and compared the results obtained using the three models. We used 2 databases: MIMIC-III and National Health Insurance Research Database (NHIRD), Taiwan. First, we trained the models and generated synthetic EHRs by using these three 3 models. We then analyzed and compared the models’ performance by using a few statistical methods (Kolmogorov–Smirnov test, dimension-wise probability for binary data, and dimension-wise average count for count data) and 2 machine learning tasks (association rule mining and prediction).
Results
We conducted a comprehensive analysis and found our models were adequately efficient for generating synthetic EHR data. The proposed models outperformed medGAN in all cases, and among the 3 models, boundary-seeking GAN (medBGAN) performed the best.
Discussion
To generate realistic synthetic EHR data, the proposed models will be effective in the medical industry and related research from the viewpoint of providing better services. Moreover, they will eliminate barriers including limited access to EHR data and thus accelerate research on medical informatics.
Conclusion
The proposed models can adequately learn the data distribution of real EHRs and efficiently generate realistic synthetic EHRs. The results show the superiority of our models over the existing model.
Keywords: electronic health records (EHRs), synthetic data generation (SDG), generative adversarial networks (GANs), Wasserstein GAN with gradient penalty (WGAN-GP), boundary-seeking GAN (BGAN)
BACKGROUND AND SIGNIFICANCE
Patient electronic health records (EHRs) contribute considerably to the medical industry and to research on topics such as developing medical software, developing new drugs, investigating diseases, and inventing cure and preventive measures for advancing medical informatics and healthcare. However, EHR data are not always freely available. The main reason is that they often consist of sensitive or regulated medical information about patients. In general, patients are not comfortable disclosing their personal data. When real EHRs are not available, healthcare organizations usually generate anonymized data by using de-identification methods.1 However, de-identification techniques such as k-anonymity, l-diversity, and t-closeness are not robust against re-identification attacks.2,3 Owing to the legal, privacy, and security concerns surrounding medical data and limited access to them, the healthcare sector lags behind other sectors in terms of employing information technology, data exchange, and interoperability.4
To circumvent these challenges, an alternative method is to generate realistic synthetic data. The advantages of using synthetic data include that they are artificially created and hence there is no explicit mapping between real and synthetic data. For this reason, unlike de-identified data, synthetic data stay resistant to re-identification. If synthetic data can carry attributes similar to actual data, it must help companies and researchers in public use of information without the hassle of obtaining real data. Some notable works on synthetic data generation (SDG) across a wide range of domains can be found in the literature.4–8 However, many such methods often are disease-specific, not realistic, work on only several variables of EHR data, or yet have a privacy concern. For example, an early innovative method, EMERGE, developed by Lombardo and Moniz5and later improved by Buczak et al.6 generates synthetic EHR data for an outbreak illness of interest (tularemia) but is potentially susceptible to re-identification. McLachlan and et al. developed an approach7 that uses a health incidence statistics (HIS)- and clinical practice guidelines (CPG)-based CareMap for generating synthetic EHRs. The main problem with this approach is that they did not use any real EHR data and hence need further experiments to guarantee the realistic properties. Park et al. conducted a good work8 related to our research, but it can handle only a few dimensions of binary data. Very recently, an excellent framework of SDG named Synthea4 has been developed to provide risk-free EHR data suited to industrial, research, and educational uses, but it is still not validated to work on diverse diseases and treatment modules. McLachlan in the paper9 also performs a comprehensive domain analysis and validation of different SDG approaches. However, it is still a challenging problem to generate realistic synthetic EHR data. In addition to preserving statistical features of the real data, synthetic data should verify its functionality for relevant applications. For instance, as Choi et al. investigated in the research,10 in practice, the resulting synthetic EHR data are often not sufficiently realistic for machine learning tasks, eg, predictive modeling. The goal of our research is to address all the issues mentioned above and propose a general model without focusing on any specific disease, number of dimensions, or size of data. The model will be suitable for generating realistic synthetic EHR data that will be statistically sound as well as good enough for machine learning tasks.
Recently, generative adversarial networks (GANs)11— types of neural networks—have attracted considerable attention from both researchers and developers because of their remarkable performance in generating high-quality synthetic images in an adversarial manner that may mislead a person into accepting such images as original images. A GAN comprises 2 neural networks: a generator (G) for generating fake but realistic images, and discriminator (D) for predicting (distinguishing) whether the input image is real or fake. Through the 2 competing G and D networks, a GAN can generate synthetic images that are nearly indistinguishable from the real images. Leveraging this power of creating realistic synthetic images, GANs have been successfully applied in many applications such as image generation,12–15 text-to-image synthesis,16,17 image-to-image translation,18–20 video generation,21,22 music generation,23 etc. All these works assert that GAN is the best choice for producing realistic synthetic samples. As in this research, our objective is to create realistic synthetic EHR data, we were motivated by the amazing power of GAN and set the target to optimize it. Note that a GAN exhibits remarkable performance in generating real-valued continuous data, but it has limitations in generating discrete data.24,25 A major reason is that a GAN fails to learn the distribution of discrete data in their original form during the gradient update process in training. To overcome this limitation, Choi et al. proposed an innovative approach called medical GAN (medGAN)10 for synthesizing discrete EHR data. They incorporated an autoencoder with the original GAN to learn the distribution of discrete data. Moreover, they incorporated the minibatch averaging method into the adversarial framework to prevent the problem of “mode collapse” encountered when a GAN tends to generate data with low diversity. Within the healthcare domain, the medGAN framework focuses on patients’ aggregated discrete features (eg, binary and count features) derived from longitudinal EHRs for experimenting with machine learning tasks. The authors achieved performance comparable to real data on many experiments, including distribution statistics and predictive modeling task.
In this study, we aimed to create more realistic synthetic EHR data than those generated by the medGAN. We applied 2 improved design concepts of the original GAN, namely, Wasserstein GAN with gradient penalty (WGAN-GP)26 and boundary-seeking GAN (BGAN)27 as alternatives to the GAN in the medGAN framework. We call the approaches medWGAN and medBGAN, respectively. The main contributions of the present study are as follows:
We introduce 2 efficient models—medWGAN and medBGAN—by integrating WGAN-GP and BGAN, respectively, as adversarial networks to generate more realistic synthetic EHR data than those generated by the existing medGAN method.
We evaluated, compared, and analyzed the performance levels of these 3 models. We observed that the proposed medWGAN and medBGAN outperform medGAN statistically as well as in machine learning tasks (association rule mining and prediction).
MATERIALS AND METHODS
In this section, we discuss the EHR datasets used in this study, followed by a short description of the GANs, and finally, present the details of existing and proposed SDG models.
Data description: The datasets used in this study were obtained from 2 sources. The first source was the Medical Information Mart for Intensive Care (MIMIC-III) database,28 a freely available public database comprising de-identified EHRs associated with approximately 60K patient admissions to the critical care units of the Beth Israel Deaconess Medical Center between 2001 and 2012. MIMIC-III contains various types of health-related data, of which we used patients’ diagnoses data (DIAGNOSES_ICD) and procedures (PROCEDURES_ICD) data, coded using the International Statistical Classification of Diseases and Related Health Problems (ICD) system.29 In this study, we investigated 2 different MIMIC-III datasets: 1 dataset consists of diagnoses data and the other (extended MIMIC-III) consists of both diagnoses and procedures data. The second source was the Taiwan National Health Insurance Research Database (NHIRD),30 which contains data of both patients and medical facilities under the National Health Insurance program. Access to this NHIRD dataset is limited, but permission is provided for its use for research work in Taiwan. We used the LHID2005: Longitudinal Health Insurance Database 2005 (a subset of the NHIRD) for the years between 1996 and 2011 and extracted inpatient expenditures by admission (DD) from it. Similar to MIMIC-III, we separated patients’ diagnoses data coded using the ICD system. Note that although our datasets are of patients’ diagnoses and procedures data, these include a rich set of information of various diseases, injuries, congenital anomalies, symptoms, signs, abnormal conditions, some supplementary factors influencing health status, operations, and medical services, etc.31,32
Like medGAN, in this research, we concentrated our investigations on generating aggregated count data (how many times a patient associated with a specific ICD code of disease or procedure) and binary data (absence or presence of specific ICD codes). The use of aggregated EHR data is common in many studies for machine learning tasks.33–36 The following 2 subsections describe converting longitudinal EHR data to aggregated count and binary data.
Convert to aggregated (count) data: For a fair comparison with medGAN, we reduced the ICD codes to 3-digit codes for each dataset. Note that in the longitudinal EHR datasets, each row corresponds to a patient’s admission record of diagnoses data (MIMIC-III and NHIRD) or of diagnoses and procedures data (extended MIMIC-III), represented by ICD codes. A patient likely visits a hospital more than once, so s/he may have multiple records in the EHR data. We aggregated each patient’s longitudinal record into a single fixed-sized vector of ICD codes. Thus, we represented each dataset as a multidimensional matrix, in which a row corresponds to a patient’s record and a column to a specific ICD code (eg, diagnoses code or procedure code). Since ICD codes are aggregated by the patients, they are all count variables. The count variables indicate the number of times a patient was associated with a specific ICD code. Table 1 shows a portion of a sample count dataset. Here, all values in Table 1 are anonymized.
Table 1.
Portion of sample count dataset
| Patient ID | ICD_817 | ICD_819 | ICD_363 |
|---|---|---|---|
| AAAAAA | 2 | 4 | 5 |
| BBBBBB | 0 | 0 | 0 |
| CCCCCC | 3 | 2 | 0 |
| … | … | … | … |
| XXXXXX | 1 | 0 | 4 |
Convert to binary data: Note that all the features in our 3 datasets, MIMIC-III, extended MIMIC-III, and NHIRD, are count variables. As we would like to analyze both count and binary discrete variables, we prepared a binary version of each count dataset by converting the aggregated count variables (say ) to binary variables (say ) by using the following equation:
| (1) |
Table 2 shows a portion of a sample binary dataset derived from the corresponding count dataset in Table 1. The binary variables indicate whether a patient was associated with a specific ICD code.
Table 2.
Portion of sample binary dataset
| Patient ID | ICD_817 | ICD_819 | ICD_363 |
|---|---|---|---|
| AAAAAA | 1 | 1 | 1 |
| BBBBBB | 0 | 0 | 0 |
| CCCCCC | 1 | 1 | 0 |
| … | … | … | … |
| XXXXXX | 1 | 0 | 1 |
Statistics of datasets: Some basic statistics of the 3 datasets derived the 2 different data sources are presented in Table 3. Observe that the NHIRD dataset is larger than the MIMIC-III datasets in terms of the number of patients/records. There are 942 ICD codes in the MIMIC-III diagnoses dataset, 1651 ICD codes (diagnoses codes: 940 and procedures codes: 711) in the extended MIMIC-III dataset, and 1015 ICD codes in the NHIRD diagnoses dataset. However, as can be seen in Figure 1, the NHIRD dataset is sparser than the MIMIC-III datasets. In Figure 1(a), we plot the empirical cumulative distribution function (ECDF) of the number of unique ICD codes associated with all the patients in each dataset. In NHIRD, 70% of patients have 5 or fewer unique ICD codes, whereas, in MIMIC-III and extended MIMIC-III, the same percentage of patients have up to 13 and 18 unique ICD codes, respectively. In Figure 1(b), we compute the proportion of patients associated with each ICD code and then plot the ECDF of the proportion of patients. In NHIRD, 90% of the ICD codes (913 among 1015) are associated with only 1.31% of patients or less, whereas in MIMIC-III, 90% of the ICD codes (845 among 942) are associated with up to 2.95% of patients, and in extended MIMIC-III, 90% of the ICD codes (1487 among 1651) are associated with up to 2.17% of patients. Note that as shown in Table 3, the MIMIC-III dataset denotes only diagnoses data, whereas the extended MIMIC-III dataset denotes both diagnoses and procedures data for the onward texts, tables, and figures.
Table 3.
Basic statistics of datasets
| Statistics | MIMIC-III (diagnoses data) | Extended MIMIC-III (diagnoses + procedures data) | NHIRD, Taiwan (diagnoses data) |
|---|---|---|---|
| # of patients / records | 46 517 | 42 214 | 498 909 |
| # of unique ICD codes / dimensions | 942 | 1651 (diagnoses: 940 and procedures: 711) | 1015 |
| Avg. # of codes per patient | 13.99 | 20.17 | 8.42 |
| Max. # of codes for a patient | 540 | 610 | 687 |
| Min. # of codes for a patient | 1 | 2 | 1 |
Figure 1.
ECDFs of ICD codes and patients for MIMIC-III, extended MIMIC-III, and NHIRD datasets.
Tables 4 and 5 list the top 10 frequent ICD codes along with their meaning, frequency of occurrences, number of unique patients, and percentage of patients associated with each code in MIMIC-III and NHIRD diagnoses datasets. The detailed description of each ICD code can be searched on the following website: http://icd9.chrisendres.com/. Table 6 shows the top 10 patient data of MIMIC-III and NHIRD datasets, which include the frequency (ie, the total number of ICD codes), the total number of unique ICD codes, and percentage of unique ICD codes for each patient.
Table 4.
Top frequent ICD codes of MIMIC-III
| Top ICD codes | Meaning | Frequency | No. of patients associated with | Percent of patients associated with |
|---|---|---|---|---|
| ICD_401 | Essential hypertension | 21 329 | 18 031 | 38.76 % |
| ICD_427 | Cardiac dysrhythmias | 20 998 | 14 022 | 30.14 % |
| ICD_428 | Heart failure | 20 676 | 10 154 | 21.83 % |
| ICD_276 | Disorders of fluid, electrolyte, and acid-base balance | 20 440 | 12 645 | 27.18 % |
| ICD_250 | Diabetes mellitus | 16 454 | 10 318 | 22.18 % |
| ICD_414 | Other forms of chronic ischemic heart disease | 15 759 | 11 926 | 25.64 % |
| ICD_272 | Disorders of lipoid metabolism | 14 768 | 12 268 | 26.37 % |
| ICD_518 | Other diseases of lung | 14 608 | 11 363 | 24.43 % |
| ICD_285 | Other and unspecified anemias | 12 910 | 10 631 | 22.85 % |
| ICD_584 | Acute renal failure | 11 467 | 9536 | 20.50 % |
Table 5.
Top frequent ICD codes of NHIRD, Taiwan
| Top ICD codes | Meaning | Frequency | No. of patients associated with | Percent of patients associated with |
|---|---|---|---|---|
| ICD_250 | Diabetes mellitus | 170 162 | 44 284 | 8.88 % |
| ICD_401 | Essential hypertension | 144 662 | 66 258 | 13.28 % |
| ICD_599 | Other disorders of urethra and urinary tract | 89 524 | 47 394 | 9.50 % |
| ICD_295 | Schizophrenic disorders | 84 584 | 4622 | 0.93 % |
| ICD_486 | Pneumonia, organism unspecified | 68 484 | 41 982 | 8.41 % |
| ICD_650 | Normal delivery | 67 437 | 47 154 | 9.45 % |
| ICD_276 | Disorders of fluid, electrolyte, and acid-base balance | 66 082 | 42 940 | 8.61 % |
| ICD_414 | Other forms of chronic ischemic heart disease | 61 985 | 28 228 | 5.66 % |
| ICD_V27 | Outcome of delivery | 60 200 | 43 896 | 8.80 % |
| ICD_571 | Chronic liver disease and cirrhosis | 59 547 | 24 796 | 4.97 % |
Table 6.
Top patient data of MIMIC-III and NHIRD datasets
| SN. of top patients | MIMIC-III |
NHIRD, Taiwan |
||||
|---|---|---|---|---|---|---|
| Frequency (No. of total ICD codes) | No. of unique ICD codes | Percent of unique ICD codes | Frequency (No. of total ICD codes) | No. of unique ICD codes | Percent of unique ICD codes | |
| 1 | 540 | 88 | 9.34 % | 687 | 18 | 1.77 % |
| 2 | 362 | 85 | 9.02 % | 605 | 5 | 0.49 % |
| 3 | 361 | 44 | 4.67 % | 527 | 23 | 2.27 % |
| 4 | 360 | 70 | 7.43 % | 505 | 16 | 1.58 % |
| 5 | 359 | 61 | 6.48 % | 501 | 5 | 0.49 % |
| 6 | 332 | 74 | 7.86 % | 490 | 14 | 1.38 % |
| 7 | 326 | 79 | 8.39 % | 487 | 15 | 1.48 % |
| 8 | 323 | 42 | 4.46 % | 485 | 20 | 1.97 % |
| 9 | 316 | 77 | 8.17 % | 469 | 7 | 0.69 % |
| 10 | 293 | 64 | 6.79 % | 466 | 8 | 0.79 % |
GANs: The idea of the GAN framework by Ian J. Goodfellow et al. was first published in,11 and later they introduced it at the NIPS 2014 conference.37 Yann LeCun, Director of AI Research at Facebook and Professor at NYU, said the following in his Quora session38:
“(GANs), and the variations that are now being proposed is the most interesting idea in the last 10 years in ML, in my opinion.”
The main idea of GANs, as indicated by the authors, is to train 2 neural networks: a generative model G, which captures the distribution of the original training data, and a discriminative model D, which classifies whether a sample originates from the original data (real) or generator (fake). The training procedure for G is to fool D, ie, to maximize the probability of D making a mistake by producing high-quality fake samples. This framework resembles a 2-player minimax game.11,37,39 A commonly used analogy is that the generator (G) is akin to a forger (criminal) trying to produce counterfeit money and that the discriminator (D) is akin to the police attempting to detect the counterfeit money. The objective of the criminal is to counterfeit money, such that the police cannot discriminate the counterfeit money from real money. In contrast, the police want to detect the counterfeit money as best as possible. Formally, the minimax game between G and D with the value function V(G, D) is as follows:
11 where is the data distribution and is the simple noise distribution (eg, uniform distribution or spherical Gaussian distribution). Initially, G accepts a random prior and generates synthetic samples for the certification of D. G is then trained (updated parameters) by using the error signal from D through backpropagation. In Figure 2, the left part [Figure 2(a)] shows the main concept of the original GAN architecture.
Figure 2.
Original GAN and medGAN architecture.
medGAN: As mentioned, the original GAN can learn only the distribution of continuous values, and the authors of the medGAN framework ameliorated this limitation by leveraging the power of autoencoders.10 The general idea of an autoencoder is mapping an input dataset to an output (called reconstruction) through an internal representation or hidden layer . An autoencoder comprises 2 components: an encoder and a decoder .40 This autoencoder mechanism is widely used to learn the salient features of training samples in various modern neural network applications.41,42 In the medGAN framework, an autoencoder is used to capture the salient features of the discrete variables and decode the continuous output of G. The autoencoder is pretrained before GAN training. As shown in Figure 2(b), the continuous output of the generator is passed through the decoder . can select the appropriate distribution from and yield the discrete output . The discriminator can now determine whether this synthetic discrete sample is fake or real in a normal fashion.
Another performance-enhancing technique used in the medGAN framework is minibatch averaging. Occasionally, in a GAN, G with different random priors may produce the same synthetic output rather than diverse outputs because of the min-max optimization strategy of the GAN instead of max-min.39 In the medGAN framework, minibatch averaging mitigates this “mode collapse” problem and significantly improves the model performance in terms of generating discrete synthetic data.
medWGAN: In the proposed medWGAN, we employ an improved generative network called WGAN-GP instead of the general GAN. The remainder of the structure is the same as that of medGAN shown in Figure 2. The authors of the WGAN-GP model in26 claimed that the previously developed Wasserstein GAN (WGAN) model43 facilitates stable training but generates low-quality samples or fails to converge in some settings owing to the use of the weight-clipping technique. To overcome these issues, they offered an alternative method of weight clipping called gradient penalty, which entails penalizing the norm of the gradient of the discriminator (critic) with respect to its input. The WGAN-GP model performs better than many GAN architectures, including the standard WGAN. Hence, in this investigation, we hypothesized that applying medWGAN to generate synthetic EHRs would yield superior performance to that achieved by applying the original medGAN.
medBGAN: This proposed model is another alternative to medGAN, and we achieved the model by replacing the traditional GAN with a new algorithm called BGAN.27 In this novel approach, a generator is trained to match a target distribution that converges toward the true distribution of the data as the discriminator is optimized. This objective can be inferred as training a generator to create samples that lie on the decision boundary of the current discriminator in training at each update. Hence, the GAN trained using this algorithm is called BGAN. This algorithm effectively works on both discrete and continuous variables and shows qualitatively superior performance levels to those of conventional GANs. Similar to medWGAN, medBGAN is expected to exhibit high performance in terms of generating synthetic EHRs.
EXPERIMENTS
In this section, we discuss our experimental setup for model training, and the process of training and generating synthetic EHRs. We also describe the methods for evaluating synthetic EHRs.
Experimental setup: We obtained the source code of medGAN from the GitHub repository on,44 trained medGAN, and applied it to generate synthetic data without changing its scripts. In our medWGAN and medBGAN, we changed a few lines of code to implement WGAN-GP and BGAN. The source code to reproduce the result is publicly available at https://github.com/baowaly/SynthEHR.
We split each of the MIMIC-III, extended MIMIC-III, and NHIRD datasets into 2 parts, namely, training and testing datasets, at a 4:1 ratio. We used the training dataset to train the models and generate the same number of synthetic EHRs. We reserved the testing dataset to test the predictive models. Most of the parameter settings of medGAN were retained in our models. Some of the common settings are listed in Table 7.
Table 7.
Experimental settings
| # of training samples of MIMIC-III | 37 213 |
| # of training samples of extended MIMIC-III | 33 771 |
| # of training samples of NHIRD | 399 127 |
| # of epochs to pre-train the autoencoder | 100 |
| # of epochs to train the model | 1000 |
| Batch size | 1000 |
| Generator size | (128, 128, 128) |
| Discriminator size | (256, 128, 1) |
Training the models: We further split the training data into training and validation subsets by a 9:1 ratio. We pre-train the autoencoder for 100 epochs using the training subset and for every epoch we report the training and validation loss, which is defined as binary-cross entropy for binary variables and mean squared error for count variables. From the training curve, we observe that 100 epochs are sufficient, and there is no overfitting.
After pre-training the autoencoder, we copy the decoder part and cascade it to be the last layer of the generator G, and train the GAN networks for 1000 epochs using the 90% training subset. For every epoch, we use the remaining 10% validation subset to check the performance (accuracy and AUC) of the discriminator D as a binary classifier. More importantly, we use the generator G to randomly generate synthetic data for every 10 epochs during the training process, and perform some sanity checks on these temporarily generated data, such as dimension-wise averages and number of nonzero dimensions. As the training process progresses, we observe that the quality of the temporarily generated synthetic data becomes better and better with all checking items become stable after 700∼800 epochs in all cases.
We examined different numbers of discriminator and generator training cycles, which we defined as the discriminator-to-generator ratio, to update them for each training epoch. Based on the correlation coefficients between the dimension-wise averages of training data and final synthetic data, we set this ratio to 2:1 for medGAN and medWGAN, and 5:1 for medBGAN.
Generation of synthetic binary EHRs: We trained the models and generated synthetic data with sizes being the nearest multiples of the batch size in the training samples (Table 3), ie, 37 000, 33 000, and 399 000 samples from MIMIC-III, extended MIMIC-III, and NHIRD, respectively. The raw generated data values were continuous in the range of 0 to . We converted them to binary (0 or 1) through rounding.
Generation of synthetic count EHRs: Similar to the binary samples, for count variables, we used the same number of training samples to train the models and generate synthetic data. However, the raw generated data values were any continuous nonnegative numbers. We rounded the continuous values of the synthetic data to the nearest integer values.
System information and computation time: Our computing server was equipped with 2 Intel Xeon E5-2667 (each with 8 physical cores), 512GB RAM, 8 Nvidia GeForce GTX 1080 Ti’s, and CUDA 8.0; although we used a single GPU at a time for training the models. We implemented our methods with TensorFlow 1.4. The average running time required to train the models and generate the synthetic data was 1.88 hours for MIMIC-III, 2.29 hours for extended MIMIC-III, and 20.12 hours for NHIRD datasets.
Methods for evaluating synthetic EHRs: After the generation of the synthetic EHRs, the obvious issue was to evaluate these generated data and compare them with the real EHRs. For these purposes, we employed some evaluation methods from 2 different perspectives as follows.
Statistical methods: As a basic sanity check to ensure whether our models learned the distribution of each dimension acceptably, we calculated the dimension-wise probability for binary data and dimension-wise average count for count data, and performed the dimension-wise Kolmogorov–Smirnov test (K–S test).
Dimension-wise probability: This refers to the Bernoulli success probability of each dimension (disease or procedure code) in the binary dataset. The dimension-wise probability is computed using the following formula:
| (2) |
Dimension-wise average: This refers to the column average of each dimension (disease or procedure code) in the count dataset. The dimension-wise average is calculated using the following formula:
| (3) |
Dimension-wise K–S test: We performed the K–S test on 2 data samples (synthetic data and real data) to examine whether the 2 data samples originate from the same distribution. In the K–S test, the statistic is calculated by finding the maximum absolute value of the differences between 2 samples’ cumulative distribution functions.45 The null hypothesis is that both samples originate from a population with the same distribution. In our experiment, we rejected the null hypothesis with a low P-value (typically ≤ 0.05). More details of the K–S test is discussed in the Results section.
Machine learning methods: We applied association rule mining and dimension-wise prediction to test how interdimensional relationships are preserved in the synthetic data.
Association rule mining: Association rule mining such as Apriori is widely used on EHR data to identify associations and interpretable patterns among clinical concepts (medications, laboratory results, and problem diagnoses).46–48 We employed this rule-based machine learning method for discovering some strong associations or relations among variables in both real and synthetic datasets. We checked whether the relations found in the real dataset were present in the corresponding synthetic dataset. For simplicity, we considered only one-to-one relationships with all rules having a length of 2. For MIMIC-III and NHIRD, we set the parameters of the Apriori algorithm (support and confidence thresholds) to be the values that yield roughly 50∼200 rules from the real dataset and use the same parameters for synthetic datasets generated by the 3 GAN models. To compare the rules found from each of the real datasets to the rules found from the corresponding synthetic dataset, we used several metrics such as precisions and recalls. Precision is defined as the number of common rules found in both real and synthetic datasets divided by the number of rules found in the synthetic dataset, and recall is defined as the number of common rules found in both real and synthetic datasets divided by the number of rules found in the real dataset.
Dimension-wise prediction: As an indirect means of testing interdimensional relationships in synthetic data, we performed a prediction task for each ICD code. We applied 3 popular machine learning methods, logistic regression, random forest, and support vector machine (SVM), which are commonly used for predictive modeling on EHR data.34–36,46,49 We compared dimension-wise prediction results of predictive models trained on synthetic data with those of the corresponding real data. To describe more specifically, suppose that we have totally dimensions (disease or procedure codes), where for MIMIC-III, for extended MIMIC-III, and for NHIRD. The predictive algorithm considers a dimension at a time as the target or dependent variable for prediction (ie, whether this disease or procedure may occur), and the remaining dimensions as the features or independent variables . Note that, for the count dataset, the target variable is converted into binary using the same technique as in Equation 1. In this way, we built predictive models for each disease or procedure using both real and synthetic datasets, and these models were subsequently applied to the heldout testing data to obtain performance scores (F1 scores). To compare prediction results of the real and synthetic datasets, we computed correlation coefficients (CCs) and the root-mean-square errors (RMSEs) by using all F1 scores across all dimensions, as explained in detail in the following sections.
RESULTS
As mentioned in previous sections, we used the binary and count versions of MIMIC-III, extended MIMIC-III, and NHIRD datasets. We applied 3 different generative models, namely, medGAN, medWGAN, and medBGAN, separately to the datasets to generate synthetic data. The performance levels of the 3 models in terms of producing synthetic EHRs are discussed in this section.
Dimension-wise probability: Figure 3 shows the dimension-wise probability performance of the 3 different generative models for MIMIC-III, extended MIMIC-III, and NHIRD synthetic binary data. Each scatterplot displays the performance of 1 generative model. In the scatterplots, each dot represents one ICD code. The x-axis represents the Bernoulli success probability of each disease or procedure (ICD code) in real data, and the y-axis represents the success probability of each disease or procedure (ICD code) in synthetic data. The diagonal line indicates the ideal case in which the performance of synthetic data is identical to that of real data. To measure the performance of each generative model numerically, we use CCs and RMSEs between real and synthetic data. The plots in Figures 3(a), (b), and (c) show similar trends of dimension-wise probability for MIMIC-III, extended MIMIC-III, and NHIRD binary data. The proposed medWGAN and medBGAN yield slightly superior performance to the baseline model medGAN, but the performances are very close to the highest mark (100%). Among the 3 models, medBGAN has the best performance.
Figure 3.
Scatterplots of dimension-wise probability results of real binary data (x-axis) vs. synthetic counterpart (y-axis) produced by the 3 generative models.
Dimension-wise average count: Figure 4 shows the dimension-wise average count of the 3 different generative models for MIMIC-III, extended MIMIC-III, and NHIRD synthetic count data. Each scatterplot displays the performance of 1 generative model. In the scatterplots, each dot represents 1 ICD code. The x-axis represents the average count of each disease or procedure (ICD code) in real data, and the y-axis represents the average count of each disease or procedure (ICD code) in synthetic data. According to Figures 4(a) and (b) for MIMIC-III and extended MIMIC-III count data, both medWGAN and medBGAN show a small improvement compared with medGAN. However, for NHIRD count data in Figure 4(c), only medBGAN outperforms medGAN, but the outputs of medGAN and medWGAN are almost identical.
Figure 4.
Scatterplots of dimension-wise average count results on real count data (x-axis) vs. synthetic counterpart (y-axis) produced by the 3 generative models.
K–S test results: We applied the dimension-wise K–S test to examine whether a specific sample (say ) of synthetic data and the corresponding sample (say ) of the real data with the same dimension name originate from a population with the same distribution (1 or 0). Then, we calculated the total percentage of similarity between each synthetic dataset and the corresponding real dataset. The derived results are summarized in Table 8. Table 8 shows the percentage of similarity between synthetic data generated by the 3 generative models and their real data counterparts. We observed that similar to the previous statistical results, the proposed medWGAN and medBGAN outperform medGAN. In most cases, medBGAN has the best performance. The medWGAN exhibits the best result only for MIMIC-III and extended MIMIC-III count data.
Table 8.
K–S test results
| Dataset | Data type | Generative model | K–S test similarity |
|---|---|---|---|
| MIMIC-III | Binary | medGAN | 94.48 % |
| medWGAN | 95.97 % | ||
| medBGAN | 97.45 % | ||
| Count | medGAN | 88.64 % | |
| medWGAN | 95.12 % | ||
| medBGAN | 89.70 % | ||
| Extended MIMIC-III | Binary | medGAN | 95.34 % |
| medWGAN | 96.49 % | ||
| medBGAN | 97.64 % | ||
| Count | medGAN | 93.46 % | |
| medWGAN | 96.24 % | ||
| medBGAN | 94.12 % | ||
| NHIRD, Taiwan | Binary | medGAN | 92.12 % |
| medWGAN | 76.35 % | ||
| medBGAN | 95.86 % | ||
| Count | medGAN | 83.35 % | |
| medWGAN | 80.59 % | ||
| medBGAN | 86.31 % |
Association rule mining: As we mentioned in the Experiments section, our main purpose for association rule mining in this study is to examine how interdimensional relationships are preserved in synthetic data, not to explore the best performance in terms of finding the most number of rules of comorbidities in real data. Therefore, we tried several sets of parameters with minimum support of 5% to 10% and confidence of 40% to 50%. We got almost the same results in evaluating interdimensional relationships between real data and synthetic data (defined by precision/recall) in all cases; therefore, we chose to show 1 evaluation result (Table 9) here that produced roughly 50∼200 rules from the real datasets. We found 72 rules from the MIMIC-III real dataset and 154 rules from the extended MIMIC-III real dataset, using the Apriori algorithm by setting minimum support = 0.05, minimum confidence = 0.50, minimum length = 2, and maximum length = 2. As for NHIRD, which is sparser and larger than MIMIC-III, we set minimum support = 0.01, minimum confidence = 0.40, minimum length = 2, and maximum length = 2, and found 63 rules from the real dataset. We maintained this same parameter setting for the corresponding synthetic datasets. The number of rules found in all synthetic datasets, as well as the precisions and recalls, are summarized in Table 9.
Table 9.
Association rule mining results
| Dataset | No. of extracted rules in real data | Generative model | No. of extracted rules in synthetic data | No. of matched rules in synthetic data | Precision | Recall |
|---|---|---|---|---|---|---|
| MIMIC-III | 72 | medGAN | 180 | 61 | 0.3388 | 0.8472 |
| medWGAN | 64 | 52 | 0.8125 | 0.7222 | ||
| medBGAN | 153 | 67 | 0.4379 | 0.9305 | ||
| Extended MIMIC-III | 154 | medGAN | 274 | 134 | 0.4890 | 0.8701 |
| medWGAN | 201 | 142 | 0.7064 | 0.9220 | ||
| medBGAN | 229 | 150 | 0.6550 | 0.9740 | ||
| NHIRD, Taiwan | 63 | medGAN | 1350 | 56 | 0.0414 | 0.8888 |
| medWGAN | 62 | 50 | 0.8064 | 0.7936 | ||
| medBGAN | 520 | 60 | 0.1153 | 0.9523 |
MIMIC-III: As we show in Table 9, under the same settings of parameters, medWGAN yields the highest precision and medBGAN yields the highest recall for the MIMIC-III dataset. In this case, we observe that both the proposed medWGAN and medBGAN outperform the original medGAN. The association rule mining on the extended MIMIC-III dataset outputs results similar to the MIMIC-III.
NHIRD, Taiwan: Similar to MIMIC-III, we observe for NHIRD that medWGAN yields the highest precision and medBGAN yields the highest recall. Hence, we can conclude that our models outperform medGAN.
From the association rule mining, it is clear that medBGAN is able to reproduce most of the rules seen in the real data and hence it outputs the best recall (93.05% for MIMIC-III, 97.40% for extended MIMIC-III, and 95.23% for NHIRD). In contrast, medWGAN generates the least number of spurious rules in the synthetic data, and hence it outputs the best precision (81.25% for MIMIC-III, 70.64% for extended MIMIC-III, and 80.64% for NHIRD). Note that although medBGAN shows low precision for NHIRD data, it performs better than medGAN.
Dimension-wise prediction performance: This part involves determining how well our synthetic data created by the generative models perform compared with the real data in the machine learning prediction task. Here, we show the dimension-wise prediction performance of both binary and count variables for MIMIC-III, extended MIMIC-III, and NHIRD synthetic data using each of the 3 aforementioned predictive models.
Figure 5 shows the dimension-wise prediction performance of the 3 generative models obtained from the results of the logistic regression model trained on MIMIC-III, extended MIMIC-III, and NHIRD synthetic binary data and the corresponding real data. In the scatterplots, each dot represents 1 ICD code. The x-axis represents the F1 scores of the logistic regression model trained on the real binary data, and the y-axis represents the F1 scores of the logistic regression model trained on the synthetic binary data. Regarding the prediction results for MIMIC-III binary data in Figure 5(a), for extended MIMIC-III binary data in Figure 5(b), and for NHIRD binary data in Figure 5(c), both medWGAN and medBGAN outperform medGAN. Notably, medBGAN shows the highest performance of all generative models.
Figure 5.
Scatterplots of dimension-wise prediction results (F1-scores) of logistic regression model trained on real binary data (x-axis) vs. synthetic counterpart (y-axis) produced by the 3 generative models.
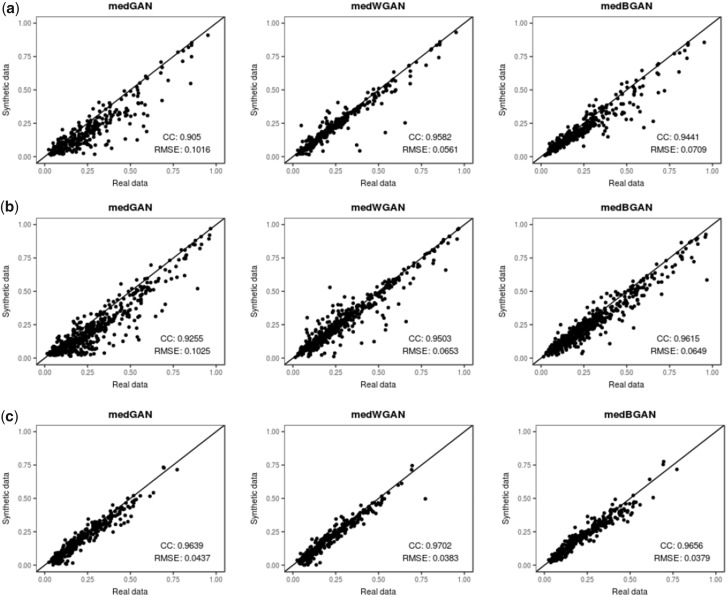
Figure 6 shows the dimension-wise prediction performance of the 3 generative models obtained from the results of the logistic regression model trained on MIMIC-III, extended MIMIC-III, and NHIRD synthetic count data and the corresponding real data. In the scatterplots, each dot represents 1 ICD code. The x-axis represents the F1 scores of the logistic regression model trained on the real count data, and the y-axis represents the F1 scores of the logistic regression model trained on the synthetic count data. Regarding the dimension-wise prediction performance for MIMIC-III count data in Figure 6(a) and for extended MIMIC-III count data in Figure 6(b), both medWGAN and medBGAN outperform medGAN, but medWGAN has the best performance for MIMIC-III, and medBGAN has the best performance for extended MIMIC-III, although they are very close in both cases. In contrast, for NHIRD count data in Figure 6(c), medWGAN has a slightly higher performance level than those of the other models, but we observe no significant differences among these 3 generative models.
Figure 6.
Scatterplots of dimension-wise prediction results (F1-scores) of logistic regression model trained on real count data (x-axis) vs. synthetic counterpart (y-axis) produced by the 3 generative models.
We evaluated the prediction results of the other 2 machine learning classifiers, random forest and SVM, in a similar fashion as we did for the logistic regression method as discussed above. The prediction performances of the 3 generative models obtained from the results (F1 scores) of the 3 predictive classifiers are shown in Table 10. In the random forest prediction results, we see that medBGAN shows better results than the remaining 2 generative models, except in extended MIMIC-III and NHIRD count datasets. In SVM predictions, medBGAN always outperforms the other generative models, although in some cases, the results are very close. Table 11 summarizes the prediction performances, which shows the best generative models of the prediction tasks on various synthetic data. From Tables 10 and 11, we can say that our models (medBGAN and medWGAN) outperform the baseline model medGAN for each of the 3 predictive modeling tasks.
Table 10.
Prediction performances of the 3 generative models
| Dataset | Data type | Generative model | Correlation coefficients (CCs) between synthetic and real data prediction results |
||
|---|---|---|---|---|---|
| Logistic regression | Random forest | SVM | |||
| MIMIC-III | Binary | medGAN | 0.9217 | 0.8907 | 0.9406 |
| medWGAN | 0.9490 | 0.9564 | 0.9505 | ||
| medBGAN | 0.9794 | 0.9733 | 0.9540 | ||
| Count | medGAN | 0.9050 | 0.9190 | 0.9469 | |
| medWGAN | 0.9582 | 0.9470 | 0.9507 | ||
| medBGAN | 0.9441 | 0.9593 | 0.9589 | ||
| Extended MIMIC-III | Binary | medGAN | 0.9298 | 0.9248 | 0.9445 |
| medWGAN | 0.9340 | 0.9450 | 0.9389 | ||
| medBGAN | 0.9724 | 0.9700 | 0.9655 | ||
| Count | medGAN | 0.9255 | 0.8985 | 0.9278 | |
| medWGAN | 0.9503 | 0.9371 | 0.9474 | ||
| medBGAN | 0.9615 | 0.9282 | 0.9553 | ||
| NHIRD, Taiwan | Binary | medGAN | 0.9030 | 0.8339 | 0.8970 |
| medWGAN | 0.9318 | 0.8471 | 0.9132 | ||
| medBGAN | 0.9609 | 0.9232 | 0.9705 | ||
| Count | medGAN | 0.9639 | 0.9325 | 0.9750 | |
| medWGAN | 0.9702 | 0.9325 | 0.9520 | ||
| medBGAN | 0.9656 | 0.9282 | 0.9756 | ||
Table 11.
Summary of prediction performances
| Dataset | Data type | Best generative model of prediction |
||
|---|---|---|---|---|
| Logistic regression | Random forest | SVM | ||
| MIMIC-III | Binary | medBGAN | medBGAN | medBGAN |
| Count | medWGAN | medBGAN | medBGAN | |
| Extended MIMIC-III | Binary | medBGAN | medBGAN | medBGAN |
| Count | medBGAN | medWGAN | medBGAN | |
| NHIRD, Taiwan | Binary | medBGAN | medBGAN | medBGAN |
| Count | medWGAN | medWGAN | medBGAN | |
DISCUSSION
A summary of our evaluation results is presented in Table 12. The table indicates the best model for each evaluation criterion of the synthetic datasets. Clearly, in each case of the evaluations, our models, either medBGAN or medWGAN, outperform the baseline model medGAN. As mentioned in the Results section, in very few cases, the improvement offered by the proposed models was not significant; nevertheless, in most cases, we obtained impressive results for both binary and count data.
Table 12.
Results summary
| Dataset | Data type | Evaluation criteria | Best generative model |
|---|---|---|---|
| MIMIC-III | Binary | Dimension-wise probability performance | medWGAN/medBGAN |
| K–S test | medBGAN | ||
| Association rule mining | medWGAN/medBGAN | ||
| Dimension-wise prediction performance | medBGAN | ||
| Count | Dimension-wise average count | medWGAN/medBGAN | |
| K–S test | medWGAN | ||
| Dimension-wise prediction performance | medBGAN | ||
| Extended MIMIC-III | Binary | Dimension-wise probability performance | medWGAN/medBGAN |
| K–S test | medBGAN | ||
| Association rule mining | medWGAN/medBGAN | ||
| Dimension-wise prediction performance | medBGAN | ||
| Count | Dimension-wise average count | medWGAN/medBGAN | |
| K–S test | medWGAN | ||
| Dimension-wise prediction performance | medBGAN | ||
| NHIRD, Taiwan | Binary | Dimension-wise probability performance | medBGAN |
| K–S test | medBGAN | ||
| Association rule mining | medWGAN/medBGAN | ||
| Dimension-wise prediction performance | medBGAN | ||
| Count | Dimension-wise average count | medBGAN | |
| K–S test | medBGAN | ||
| Dimension-wise prediction performance | medWGAN |
MIMIC-III vs. Extended MIMIC-III: There was an important purpose of using 2 different MIMIC-III datasets in this study to investigate whether our proposed models can be applied to the dataset of several EHR data types simultaneously. For this reason, in addition to the MIMIC-III diagnoses dataset, we employed the extended MIMIC-III dataset, which included both diagnoses and procedures EHR data. Table 12 shows that the evaluation results of the extended MIMIC-III dataset are the same as the MIMIC-III dataset, which proves the effectiveness of our models.
medWGAN vs. medBGAN: A comparison of the proposed models is warranted. For MIMIC-III data, medWGAN outperforms medBGAN only in the K–S test on count data, and medBGAN yields the best performance for all the remaining evaluations. On the contrary, in NHIRD data, medBGAN shows the best performance in all cases except in the prediction of count data. However, the improvement of medWGAN was trivial. In association rule mining, each model shows better performance than the other does from different perspectives.
Because in a few cases, medWGAN shows little improvement or comparable performances to medBGAN, we analyzed its performance from a different perspective here, ie, the total number of all-zero dimensions in the synthetic data. While generating the synthetic data, we observed that in our real dataset, some diseases rarely occurred among the patients, ie, some dimensions (columns) consisted of all zeros or very few nonzero values. For these dimensions, the models might have generated synthetic data with some all-zero dimensions. Table 13 lists these statistics for count datasets, indicating that for the synthetic datasets with count variables, medWGAN generates more dimensions with all zeros than medBGAN and medGAN do.
Table 13.
All-zero dimensions
| Dataset (count variables) | # of dimensions with all zeros |
||
|---|---|---|---|
| MIMIC-III (total dimensions: 942) | Extended MIMIC-III (total dimensions: 1651) | NHIRD, Taiwan (Total dimensions: 1015) | |
| Original (real) data | 6 (0.64 %) | 26 (1.57 %) | 5 (0.49 %) |
| medGAN synthetic data | 324 (34.39 %) | 620 (37.55 %) | 172 (16.94 %) |
| medWGAN synthetic data | 607 (64.43 %) | 1135 (68.75 %) | 694 (68.37 %) |
| medBGAN synthetic data | 163 (17.30 %) | 453 (27.44 %) | 128 (12.61 %) |
The all-zero dimensions produced by medWGAN are 607 (64.43%) for MIMIC-III data, 1135 (68.75%) for extended MIMIC-III data, and 694 (68.37%) for NHIRD data. Although medGAN generates good results here, as shown in Table 13, it did not exhibit superior performance to medWGAN in the other previous evaluations. By contrast, medBGAN performs the best, as well as producing fewer numbers of all-zero dimensions (17.30% for MIMIC-III, 27.44% for extended MIMIC-III, and 12.61% for NHIRD datasets). Therefore, overall, we can conclude that the proposed medBGAN outperforms both medWGAN and medGAN.
Implications and Limitations: This research has been conducted to build realistic and useful discrete synthetic EHR data leveraging the idea of improved GANs. In this extensive work, in addition to the basic statistical analysis, we applied 3 popular machine learning methods for predictive modeling and 1 widely used method (Apriori) for association rule mining. The whole study was conducted on 3 diverse EHR datasets—MIMIC-III (diagnoses data), extended MIMIC-III (diagnoses + procedures data), and NHIRD (diagnoses data)—in terms of their source, size, and sparsity. The evaluation results of all the conducted experiments prove the superiority of our models over the existing medGAN model in producing realistic synthetic EHR data. It also ensures us that the generated synthetic data are good enough for machine learning tasks. Note that in this study, we investigated patients’ diagnoses and procedures data as a case study. However, our proposed method is not restricted to these data because we did not use any diagnosis-specific or procedure-specific knowledge during GAN training. Additionally, the original GAN-based methods perform well to generate continuous data. Therefore, as a general method, our model can be used to generate any realistic EHR data, even beyond the medical domain.
The use of our generated synthetic data can help to mitigate the difficulty in obtaining real EHR data for research purposes. We hope this study will play a significant role in forwarding the development of medical research and technology.
Privacy consideration: For privacy consideration, as we mentioned in the first section, synthetic data are artificially created, and hence there is no explicit mapping between real and synthetic data. For this reason, intuitively, we can say that our generated synthetic data also stay resistant to re-identification. More importantly, Choi et al. performed a formal assessment of medGAN’s privacy risks based on both attributed disclosure and presence disclosure in the synthetic dataset.10 The privacy experiments showed that medGAN generates diverse synthetic samples that reveal little information to potential attackers. As we used an architecture similar to medGAN, it inherits privacy preservation in our models. We will explore this issue in the future.
CONCLUSION
We propose 2 variations of the medGAN model, namely, medWGAN and medBGAN, which can adequately learn the distribution of real-world EHRs and exhibit remarkable performance in generating realistic synthetic EHRs for both binary and count variables. We comprehensively analyzed the synthetic EHR data generated by the 3 generative models and compared their evaluation results with real EHR data. Based on this investigation, we conclude that the proposed models outperformed the existing medGAN, and that among these 3 models, medBGAN performed the best.
FUNDING
This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.
CONTRIBUTORS
Mrinal Kanti Baowaly primarily contributed to the conception and design of the work; the acquisition, analysis, and interpretation of data; implementation of the work; finding out the results; and evaluation and analysis of the results. He drafted the work. Chia-Ching Lin substantially contributed to the analysis and interpretation of data and helped the implementation of the work and finding out the results. He also helped to draft the work. Dr Chao-Lin Liu and Dr Kuan-Ta Chen both significantly contributed to the work supervising the whole research and advising in drafting the work. All authors revised the work critically for important intellectual content and approved the final version submitted to JAMIA. All of them agree to be accountable for all aspects of the work and will help in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Conflict of interest statement. The authors have no competing interests to declare.
REFERENCES
- 1.Office for Civil Rights. Guidance Regarding Methods for De-identification of Protected Health Information in Accordance with the Health Insurance Portability and Accountability Act (HIPAA) Privacy Rule. U.S. Department of Health and Human Services, 20 November 2013. https://www.hhs.gov/hipaa/for-professionals/privacy/special-topics/de-identification/index.html. Accessed March 12, 2017.
- 2. Emam KE, Jonker E, Arbuckle L, et al. A systematic review of re-identification attacks on health data. PLoS One 2011; 6 (12): e28071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Emam KE, Rodgers S, Malin B.. Anonymising and sharing individual patient data. Br Med J 2015; 350: h1139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Walonoski J, Kramer M, Nichols J, et al. Synthea: an approach, method, and software mechanism for generating synthetic patients and the synthetic electronic health care record. J Am Med Inform Assoc 2018; 25 (3): 230–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Lombardo JS, Moniz LJ.. A method for generation and distribution of synthetic medical record data for evaluation of disease-monitoring systems. Johns Hopkins APL Tech Digest 2008; 27 (4). [Google Scholar]
- 6. Buczak AL, Babin S, Moniz L.. Data-driven approach for creating synthetic electronic medical. BMC Med Inform Dec Mak 2010; 10 (1): 59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. McLachlan S, Dube K, Gallagher T.. Using the CareMap with health incidents statistics for generating the realistic synthetic electronic healthcare record In: 2016IEEE International Conference on Healthcare Informatics (ICHI ), Chicago, IL, USA, 2016. [Google Scholar]
- 8. Park Y, Ghosh J, Shankar M.. Perturbed Gibbs samplers for generating large-scale privacy-safe synthetic health data In: 2013 IEEE International Conference on Healthcare Informatics. Philadelphia, PA, USA, 9–11 Sept. 2013. [Google Scholar]
- 9. McLachlan S. Realism in Synthetic Data Generation. Palmerston North, New Zealand: Massey University; 2017. [Google Scholar]
- 10. Choi E, Biswal S, Malin B, et al. Generating Multi-label Discrete Patient Records using Generative Adversarial Networks. arXiv:1703.06490, 17 June 2017. [Google Scholar]
- 11. Goodfellow IJ, Pouget-Abadie J, Mirza M, et al. Generative Adversarial Networks. arXiv:1406.2661, June 2014. [Google Scholar]
- 12. Salimans T, Goodfellow I, Zaremba W, et al. Improved Techniques for Training GANs. arXiv:1606.03498, 10 June 2016. [Google Scholar]
- 13. Radford A, Metz L, Chintala S.. Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks. arXiv:1511.06434, 7 January 2016. [Google Scholar]
- 14. Jin Y, Zhang J, Li M, Tian Y.. Towards the Automatic Anime Characters Creation with Generative Adversarial Networks. arXiv:1708.05509, 18 August 2017. [Google Scholar]
- 15. Wang T-C, Liu M-Y, Zhu J-Y, et al. High-Resolution Image Synthesis and Semantic Manipulation with Conditional GANs. arXiv:1711.11585, 30 November 2017. [Google Scholar]
- 16. Reed S, Akata Z, Yan X, et al. Generative Adversarial Text to Image Synthesis. arXiv:1605.05396, 5 June 2016. [Google Scholar]
- 17. Zhang H, Xu T, Li H, et al. StackGAN: Text to Photo-Realistic Image Synthesis with Stacked Generative Adversarial Networks. arXiv:1612.03242, 5 August 2017. [DOI] [PubMed] [Google Scholar]
- 18. Dong H, Neekhara P, Wu C, Guo Y.. Unsupervised Image-to-Image Translation with Generative Adversarial Networks. arXiv:1701.02676, 10 January 2017. [Google Scholar]
- 19. Isola P, Zhu J-Y, Zhou T, Efros AA.. Image-to-Image Translation with Conditional Adversarial Networks. arXiv:1611.07004, 22 November 2017. [Google Scholar]
- 20. Huang X, Liu M-Y, Belongie S, Kautz J.. Multimodal Unsupervised Image-to-Image Translation. arXiv:1804.04732, 12 April 2018. [Google Scholar]
- 21. Vondrick C, Pirsiavash H, Torralba A.. Generating Videos with Scene Dynamics. arXiv:1609.02612, 26 October 2016. [Google Scholar]
- 22. Tulyakov S, Liu M-Y, Yang X, Kautz J.. MoCoGAN: Decomposing Motion and Content for Video Generation. arXiv:1707.04993, 14 December 2017. [Google Scholar]
- 23. Yang L-C, Chou S-Y, Yang Y-H.. MidiNet: A Convolutional Generative Adversarial Network for Symbolic-domain Music Generation. arXiv:1703.10847, 18 July 2017. [Google Scholar]
- 24. Kusner MJ, Hernández-Lobato JM.. GANS for Sequences of Discrete Elements with the Gumbel-softmax Distribution. arXiv:1611.04051, 12 November 2016. [Google Scholar]
- 25. Yu L, Zhang W, Wang J, et al. SeqGAN: sequence generative adversarial nets with policy gradient In: Thirty-First AAAI Conference on Artificial Intelligence (AAAI-17), 2017. [Google Scholar]
- 26. Gulrajani I, Ahmed F, Arjovsky M, et al. Improved Training of Wasserstein GANs. arXiv:1704.00028, 29 May 2017. [Google Scholar]
- 27. Hjelm RD, Jacob AP, Che T, et al. Boundary-Seeking Generative Adversarial Networks. arXiv:1702.08431, 22 May 2017. [Google Scholar]
- 28. Alistair EJ, Tom PJ, Shen L, et al. MIMIC-III, a freely accessible critical care database. Scientific Data; 2016. https://www.nature.com/articles/sdata201635. Accessed October 5, 2016. [DOI] [PMC free article] [PubMed]
- 29.International Classification of Diseases, Ninth Revision, Clinical Modification (ICD-9-CM). National Center for Health Statistics (NCHS) and the Centers for Medicare & Medicaid Services (CMS. https://www.cdc.gov/nchs/icd/icd9cm.htm. Accessed June 30, 2017.
- 30.National Health Insurance Research Database, Taiwan. National Health Insurance Administration, Ministry of Health and Welfare, Taiwan. http://nhird.nhri.org.tw/en/. Accessed January 10, 2016.
- 31.Diseases and Injuries Tabular Index. National Center for Health Statistics (NCHS) and the Centers for Medicare & Medicaid Services (CMS). http://icd9.chrisendres.com/index.php? action=contents. Accessed July 10, 2017.
- 32.Procedures Index. National Center for Health Statistics (NCHS) and the Centers for Medicare & Medicaid Services (CMS). http://icd9.chrisendres.com/index.php? action=procslist. Accessed July 12, 2017.
- 33. Himes BE, Dai Y, Kohane IS, et al. Prediction of chronic obstructive pulmonary disease (COPD) in asthma patients using electronic medical records. J Am Med Inform Assoc 2009; 16 (3): 371–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Wu J, Roy J, Stewart WF.. Prediction modeling using EHR data: challenges, strategies, and a comparison of machine learning approaches. Med Care 2010; 48 (6): 106–13. [DOI] [PubMed] [Google Scholar]
- 35. Huang SH, LePendu P, Iyer SV, et al. Toward personalizing treatment for depression: predicting diagnosis and severity. J Am Med Inform Assoc 2014; 21 (6): 1069–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Teixeira PL, Wei W-Q, Cronin RM, et al. Evaluating electronic health record data sources and algorithmic approaches to identify hypertensive individuals. J Am Med Inform Assoc 2017; 24 (1): 162–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Goodfellow IJ, Pouget-Abadie J, Mirza M, et al. Generative adversarial networks. In: Neural Information Processing Systems (NIPS), 2014. [Google Scholar]
- 38. LeCun Y. What are some recent and potentially upcoming breakthroughs in deep learning. Quora, November 2017. https://www.quora.com/What-are-some-recent-and-potentially-upcoming-breakthroughs-in-deep-learning. Accessed November 03, 2017.
- 39. Goodfellow IJ. NIPS 2016 Tutorial: Generative Adversarial Networks. CoRR, vol. abs/1701.00160, 07 June 2017. [Google Scholar]
- 40. Goodfellow IJ, Bengio Y, Courville A.. Deep Learning. Cambridge, MA: MIT Press; 2016. [Google Scholar]
- 41. Vincent P, Larochelle H, Bengio Y, et al. Extracting and composing robust features with Denoising Autoencoders In: Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 2008. [Google Scholar]
- 42. Hinton GE, Salakhutdinov RR.. Reducing the dimensionality of data with neural networks. Science 2006; 313 (5786): 504–7. [DOI] [PubMed] [Google Scholar]
- 43. Arjovsky M, Chintala S, Bottou L.. Wasserstein GAN. arXiv:1701.07875, 2017. [Google Scholar]
- 44.medGAN Source Code. GitHub repository. https://github.com/mp2893/medgan. Accessed November 2017.
- 45.Kolmogorov–Smirnov test. Wikipedia. https://en.wikipedia.org/wiki/Kolmogorov%E2%80%93Smirnov_test. Accessed November 20, 2017.
- 46. Yadav P, Steinbach M, Kumar V, et al. Mining electronic health records (EHRs): a survey. ACM Comput Surv 2018; 50 (6): 1. [Google Scholar]
- 47. Wright A, Chen ES, Maloney FL, et al. An automated technique for identifying associations between medications, laboratory results and problems. J Biomed Inform 2010; 43 (6): 891–901. December [DOI] [PubMed] [Google Scholar]
- 48. Shin AM, Lee IH, Lee GH, et al. Diagnostic analysis of patients with essential hypertension using association rule mining. Healthc Inform Res 2010; 16 (2): 77–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Sun J, McNaughton CD, Zhang P, et al. Predicting changes in hypertension control using electronic health records from a chronic disease management program. J Am Med Inform Assoc 2014; 21 (2): 337–44. [DOI] [PMC free article] [PubMed] [Google Scholar]