Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2012 Oct 17.
Published in final edited form as: Nat Protoc. 2009 Jun 4;4(7):1006–1012. doi: 10.1038/nprot.2009.94

Computational reconstruction of cell and tissue surfaces for modeling and data analysis

Frederick Klauschen 1,*, Hai Qi 2, Jackson G Egen 2, Ronald N Germain 1,2, Martin Meier-Schellersheim 1,*
PMCID: PMC3474339  NIHMSID: NIHMS405718  PMID: 19536268

Abstract

We present a method for computational reconstruction of the 3-D morphology of biological objects, such as cells, cell conjugates or 3-D arrangements of tissue structures, using data from high-resolution microscopy modalities. The method is based on the iterative optimization of Voronoi representations of the spatial structures. The reconstructions of biological surfaces automatically adapt to morphological features of varying complexity with flexible degrees of resolution. We show how 3-D confocal images of single cells can be used to generate numerical representations of cellular membranes that may serve as the basis for realistic, spatially resolved computational models of membrane processes or intracellular signaling. Another example shows how the protocol can be used to reconstruct tissue boundaries from segmented two-photon image data that facilitate the quantitative analysis of lymphocyte migration behavior in relation to microanatomical structures. Processing time is of the order of minutes depending on data features and reconstruction parameters.

INTRODUCTION

The increased availability and use of advanced 3-D imaging techniques such as fluorescence confocal and multi-photon or electron tomographic microscopy has enabled researchers to investigate biological structures and processes with a high degree of spatial resolution. The applications range from high-resolution mapping of (sub-)cellular morphology and dynamic tracking of fluorescently labeled proteins in sub-cellular compartments to in situ imaging of cell population behavior1–3. Because many biological processes are closely related to and influenced by the spatial context in which they occur – information made accessible by 3-D microscopy – it is essential to include these spatial properties in the analysis of such data. Moreover, because data sets acquired in these experiments are usually large and the relevant biological objects are numerous and/or the spatial properties complex, manual analyses are laborious and frequently involve subjective choices that render them problematic for quantitative data analysis. Here, we describe the application of an approach, implemented in a user-friendly software tool, that allows for the automated three-dimensional reconstruction of the surfaces of biological objects ranging from (sub-) cellular membranes to tissue/organ boundaries and the subsequent integration of these reconstructions with automated tissue-contextual cell migration data analysis and modeling.

Introduction to Voronoi diagrams

Many different strategies for computational surface reconstruction have been developed, frequently based either on higher-order polygonal 4, 5 or triangular 6, 7 surface meshes (for a review, see e.g. 8). Most approaches were designed mainly for visualization purposes in software used to process microscopy data, as for instance in Imaris® (Bitplane). The difference between those approaches and the technique introduced here are that our approach uses adaptive resolution of surface features, can reduce artefacts resulting from lower out-of-plane resolution, and is capable of high-quality mesh generation required for computational modeling. The price that has to be paid for the combination of these advantages is that the iterative optimization procedure may cause longer processing times compared to conventional approaches if high mesh resolutions are desired. Our method, used to obtain the results published in ref. 9 is based on the geometric concept of ‘Voronoi diagrams10’ that combines the concepts of polygonal and triangular meshes and offers specific advantages for numerical simulations 11. In two dimensions, a Voronoi diagram (also called Dirichlet tesselation12) of a set of points, here called ‘vertices’, is constructed by subdividing the area containing the vertices into geometric mesh elements in such a way that the Voronoi element of each vertex comprises the region surrounding the vertex that is closer to this than to any other vertex13 (Fig. 1). Because Voronoi diagrams can be computed for arbitrary vertex distributions, their shapes can also be highly variable (Fig. 1A). There exist, however, vertex distributions for which the Voronoi diagrams have properties that are particularly desirable for computational analyses: the variation of the distances between neighboring vertices is minimized (equally spaced mesh) and the ratio of the element circumference and element area are minimal. In 2-D, these optimized Voronoi diagrams, or meshes, are hexagonal lattices (Fig. 1D). They occur naturally, for instance, in bee honeycombs, minimizing the material needed for building robust planar structures. Voronoi-like shapes generated during isotropic growth or diffusion processes starting from initial seed points, as in turtle carapaces or giraffe fur, show similar but sometimes less optimized hexagonal structures. Perfectly hexagonal structures can be viewed as limiting cases toward which ‘real’ meshes, i. e. 2-D meshes constrained by boundaries or embedded in 3-D, may evolve if appropriate algorithms are used. Such meshes are called ‘optimal’ (or also ‘high-quality’ meshes).

Figure 1.

Figure 1

Open in a new tab

Iterative Voronoi mesh optimization illustrated in 2-D plane. Voronoi cells are depicted by center point (blue) and cell border (magenta). A: Initial random distribution of vertices. B, C, D: optimized mesh after 1, 10 and 500 iterations. E: Movement of Voronoi cell centroids during optimization process indicated by grey trajectory. F: Average movement of centroids during the optimization process. The linear plot shows the relatively fast convergence after ~30 iterations. The logarithmic plot shows local maxima prominent between 200 and 400 iterations, which indicate that the final neighborhood configuration has not been reached. At more than 400 iterations the optimum hexagonal structure is accomplished and the average centroid movement falls strictly monotonously.

An important characteristic of optimal Voronoi meshes is that the center points (also called forming points) have the same coordinates as the centroids of the elements. While vertex distributions resulting in optimal Voronoi meshes can be easily generated in a two dimensional plane without boundaries or with rectangular borders, this task is nontrivial if curved boundaries are present or for curved surfaces embedded in 3-D, which is the case for computational reconstructions of cell/tissue surfaces. The computational method we describe here uses an iterative optimization algorithm that produces optimal meshes for arbitrary shapes and boundaries from arbitrary initial vertex distributions. Initial “seed” vertices are distributed randomly within the confines of the surface layer defined by a 3-dimensional binary mask created from microscopy image series (Figure 2). Then the Voronoi surface elements are computed for the initial distribution and the vertices are subsequently moved to the centroids of these elements. In the next step the Voronoi elements are recomputed for the centroids, which starts an iterative process (computation of Voronoi diagram → computation of Voronoi centroid → replacement of Voronoi center vertex with centroid ↲) that converges to an optimal Voronoi mesh with hexagonal element geometry (Figures 1E,F and 3).

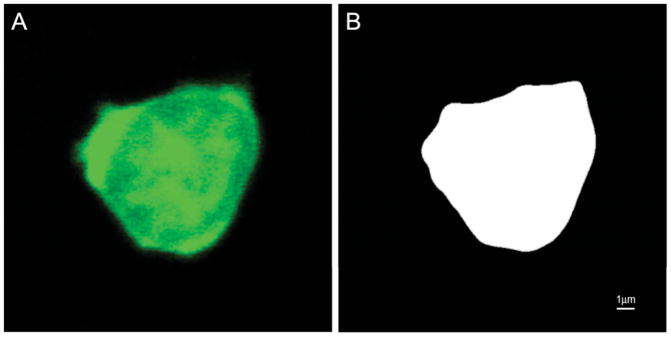
Figure 2.

Figure 2

Open in a new tab

Binary image generation from fluorescence microscopy data. A: Original confocal image (example z-slice of 3-D stack data) of a T cell; B: binary segmentation result used as input for surface reconstruction (image size: 500×500 pixel).

Our approach permits to automatically and adaptively produce optimized meshes and resolve morphological details of varying complexity with an optimal number of elements for a given desired accuracy. More precisely, our method offers two reconstruction alternatives that may also be combined. The first option requires the definition of the total number of elements/vertices used in the reconstruction. The method then iteratively optimizes the distribution of the vertices so that a uniform (high-quality) mesh is generated (Figure 4 and Box 1 ‘Description of the reconstruction algorithm’), which approximates the surface with an accuracy not lower than the average distance between neighboring vertices. The second (and default) option allows for the automatic adaptation of the reconstruction to local differences in spatial detail in the image data and ensures that a certain accuracy of the surface reconstruction is reached with a minimal number of elements (Figure 5). This approach is based on the computation of local quality measures (for instance, angles between surface elements or Euclidean vs. geodesic vertex distances) and uses local mesh refinement if quality criteria are not met (see Box 2 ‘Local adaptivity’ for details). These numerical Voronoi reconstructions are useful whenever quantitatively precise representations of spatial features have to be extracted from 3D microscopy images. Here we focus on two example applications at distinct scales of biological resolution.

Figure 4.

Figure 4

Open in a new tab

Optimizing surface reconstruction for a given number of vertices/elements (n=500) for the T cell shown in Figure 2. Blue: Lines connecting the Voronoi cell centers. A, initial arbitrary vertex distribution. B, C and D after 2, 10 and 100 optimization iterations.

BOX 1. Description of the reconstruction algorithm.

The following steps are performed automatically without any user intervention and are listed here only to present details of the algorithm.

  • 1)

    Extraction/labeling of the surface voxels.

  • 2.1)

    Initial random distribution of a number (depending on the intended resolution) of seed vertices within the surface layer defined in step 1 and

  • 2.2)

    Definition of a minimum reconstruction accuracy (optional, see below for details).

  • 3)

    Computation of the Voronoi diagram for the current vertex locations embedded in the voxel surface data. Algorithm: Assign each surface voxel the label of the closest seed vertex.

  • 4)

    Computation of the centroid for each Voronoi element. Algorithm: Compute the arithmetic means of the coordinates of all surface voxels of each Voronoi element and assign the centroid to the surface voxel closest to the mean coordinates.

  • 5)

    Replacement of the current Voronoi vertices with the centroids of the Voronoi element.

  • 6)

    Iteration of steps 3–6 for a pre-defined number of loops or until the average distance between the centroid and the Voronoi center vertex drops below a (default or user-definable) threshold.

Figure 5.

Figure 5

Open in a new tab

Automatic adaptive surface reconstruction of the T cell microscopy data shown in Figure 1, minimizing the required number of vertices/elements for a given reconstruction accuracy (ratio out-of-plane/in-plane resolution 9:1, average cell radius ~4.5μm, compare scale in Fig. 1). Blue lines: Voronoi mesh; Grey lines: Corresponding ‘dual’ triangular mesh connecting the Voronoi cell centers. A: Initial surface approximation with a small number of vertices (n=20). B, C: Optimization results after 11 (B) and 26 (C) iterations based on acute angle refinement criterion: Adaptive vertex insertion if angles between adjacent triangles are smaller than 135 degrees allows for accurately resolving morphological features while minimizing the number of surface vertices (n(final)=289) (C, D: rotation and magnification of C).

BOX 2. Local adaptivity.

The reconstruction algorithm without local adaptivity results in a homogeneous mesh, i.e., the mesh vertices are equally distributed over the surface resulting in an optimal mesh approximating the surface with a accuracy given by the mesh constant (average distance between neighboring vertices) (Supplementary Figure 1). With locally adaptive reconstruction, the surface reconstruction adaptively resolves morphological details until a certain, definable accuracy is reached. This is achieved by computing the angles between every pair of adjacent triangles. If this angle is smaller than a certain threshold, the mesh is locally refined by inserting an additional vertex at the center of the common side of the two adjacent triangles. To maintain a locally optimized grid structure, one ‘regular’ iteration step is performed following the insertion of additional vertices. This adaptivity generates surface parameterization of higher accuracy with a locally higher density of vertices in regions of higher spatial complexity, while limiting the total number of elements (Figure 5). The relevant options and parameters can be set in the MorphologyModeler Params menu.

Example applications

The first example describes surface reconstruction based on microscopy images of cellular morphology. Computational studies in cell biology increasingly take into account that many aspects of cellular function cannot be understood or modeled without proper treatment of cellular morphology14–17. Analyzing or simulating intra-cellular biochemical dynamics, such as non-isotropic reaction-diffusion processes in the cytoplasm or on the cell membrane or intra-cellular transport mechanisms, requires computational representations (spatial discretizations) of cellular morphology. The elements of high quality Voronoi meshes are particularly suitable for such discretizations because they ensure locally homogeneous mesh spacings even for complex cell morphologies and the lines connecting the Voronoi centroids are perpendicular to the element boundaries, properties that greatly facilitate mathematical analyses and simulation of diffusion and fluxes18. Because our reconstruction method can adapt its spatial resolution to the morphological properties of the cells being analyzed, we obtain high quality representations of cellular structure with a minimal number of volume elements, thereby minimizing computational costs of numerical analyses and simulations (Fig. 5).

On a slightly higher spatial scale, analyzing the dynamic organization of physically interacting cell populations in specialized tissues requires computational representations of micro-anatomical structures and cellular motion tracks. Recent advances in in-situ two-photon microscopy have facilitated the investigation of cell behavior dynamics within complex tissue environments. These technological developments have been particularly beneficial for immunological research, as the analysis of migration and interaction of leucocytes, lymphocytes, and antigen presenting cells in secondary lymphoid organs and at sites of chronic inflammation is critical for a deeper understanding of the immune response19. Because the microanatomy of secondary lymphoid organs reflects the compartmentalization of T and B cells and antigen presenting cells and provides guidance for entry, internal movement, and exit of cells, cell migration analysis must take into account the micro-anatomical context. In the tissue surface reconstruction example presented here we specifically look at germinal centers (GCs), which are organized lymphoid tissue structures where high affinity antibody responses are generated. Lymphocytes that occupy GCs mainly include antigen-specific B and T cells, while naïve B cells are largely excluded from the GC proper. Intravital 2-photon microscopy has been increasingly utilized to understand how the GC tissue structure is dynamically organized and maintained and how the trafficking of its cellular components is controlled20–22. To analyze imaging data from such studies, it is often necessary to define GC-related tissue domains. Typically, this is accomplished by manual annotation of tissue boundaries on optical sections according to relevant fluorescently-labeled tissue landmarks. Ideally, these boundaries defined on series of axially adjacent 2-D imaging planes are further digitally combined to allow visualization and mathematic description of the reconstructed tissue structure in full 3-D space (Figures 7). The tissue reconstructions generated using this protocol have been used in a recent research publication9 to quantitatively analyze the cellular migration behavior of lymphocytes in the context of germinal center tissue structure. In that study computing and comparing the speed and location/distance of a SLAM-associated-protein and wild-type lymphocytes relative to the virtual germinal center surface over each track length permitted the automatic quantification and classification of the cell behaviour. The analysis revealed that in contrast to wild-type, SAP KO T lymphocytes are incapable of crossing the border of and moving into germinal centers (see 9 for details).

Figure 7.

Figure 7

Open in a new tab

Extraction of and mask generation for germinal center (GC) region. A: Z-stack projection of two-photon microscopy images (bright: lymphocytes): B, C: Manually traced mask of germinal center region used as input for surface reconstruction. D: Reconstruction result overlaid with cell tracking data (blue: cut-plane through germinal center indicating, green: reconstructed germinal surface, red: cell track locations outside GC, light green: cell track location in GC border region). C, D: The out-of-plane resolution is 3 μm.

In addition to these types of applications, our method may improve the computational efficiency of standard surface reconstruction applications, such as morphological measurements or surface visualization, because it minimizes the number of surface elements for a given reconstruction accuracy. Conventional approaches, on the other hand, use triangular meshes with high homogeneous resolution and cannot locally adapt the mesh to surface features.

MATERIALS

Reagents

  • Image data, see Reagent Setup for details of preparation/segmentation. The Morphology Modeler requires (binary) segmented image data as input, which may be either generated manually using a standard image manipulation software such as Photoshop® (http://www.adobe.com/products/photoshop/) or GIMP (http://gimp.org) or automatically from fluorescence microscopy data using image segmentation software (e. g., 2PISA (Klauschen et al., in preparation)).

Equipment

  • Reconstruction software: The software package MoMo (Morphology Modeler) we developed and use here is available for Windows XP/Vista, MacOS X and Linux 32-/64-bit and may be obtained free of charge for non-commercial use. It can be downloaded at http://www3.niaid.nih.gov/labs/aboutlabs/psiim/computationalBiology. The surface reconstruction and cell track analysis method we present here may also be implemented using any modern programming language and the explanations of the method we present would be sufficient for that purpose.)

  • Computer hardware: The computations can be performed on most computers with current standard specifications (OpenGL capabilities are required for surface visualization), limited only by the memory required to handle 3-D microscopy data. The reconstructions shown here were performed on an Apple MacPro® Workstation with 16GB main memory (http://www.apple.com) running 64bit SuSE Linux (http://www.opensuse.org).

Reagent set up

Image data preparation

The surface reconstruction protocol described in the procedure may be used with any kind of segmented image data whose format represents an object whose surface is to be reconstructed with intensity values equal to or larger than 1 while the background pixels are zero. The images have to be provided in individual z -stack files and may have the following formats: JPEG, TIFF, or PNG. Files have to be named using a prefix followed by numbers indicating the z slice (the index format is detected automatically) and the corresponding image format suffix.

To generate the binary segmentations of the 3-D confocal microscopy images of the T cell used in our first example application, we manually defined an intensity threshold to differentiate between cell and background pixels using standard image processing software (e. g. Photoshop or GIMP) and applied that threshold to the whole z-stack (Figure 2). In case of image data of lower quality, for instance due to z-stack intensity inhomogeneities, we recommend using automatic segmentation software (see Reagents). To define binary masks of the germinal center area on individual imaging planes, which serve as the input for the tessellation program, we took advantage of the fact that naive B cells as a population are substantially excluded from GCs (Figure 7A). Therefore, fluorescent signals associated with naïve B cells were time-averaged for each imaging time series, and the follicular area and approximation of the GC–mantle border on individual optical sections were manually marked using the Photoshop mask function. Such marked images were then transformed into binary images in Photoshop, with pixel size and dimension maintained. The resulting z-stack of segmented germinal center masks essentially represents the average configuration of the visualized GC during the imaging period (Figure 7B,C).

PROCEDURE

Surface Reconstruction (using the Morphology Modeler MoMo)

  • 1

    Start the Morphology Modeler software MoMo.

  • 2

    In the SurfParam menu select item Load Microscopy Data.

  • 3

    Select the first slice of the data set to load the complete image series and click ‘open’.

  • 4

    Choose between homogeneous vertex distribution or locally adaptive surface reconstruction. For homogeneous reconstruction, set the number of vertices/mesh elements. For locally adaptive reconstruction, set the refinement threshold angle parameter (between −1.0 for minimum and +1.0 for maximum refinement).

    ?Troubleshooting.

  • 5

    Enter the z stack factor, which is the ratio of the out-of-plane and in-plane resolution.

  • 6

    Select if top or bottom elements should be labeled in case the z stack does not fully contain the microanatomical object.

  • 7

    The software will automatically check if input data contains more than one class label. If data contains only background and a single object/class label the program automatically continues to step 8 and no user action is required. If data contains more than one class label choose a class label for reconstruction or enter ‘0’ to merge all labels.

  • 8

    In the SurfParam menu select item Save Surface Tesselation to save the result.

  • 9

    Rotate the mouse wheel to visualize the surface and hold the left mouse button clicked and move the mouse to rotate the surface rendering.

Load and visualize surface

  • 10

    In the SurfParam menu select item Load Surface Tesselation to load surface.

  • 11

    Scroll mouse wheel to visualize surface.

  • 12

    In the GridVis menu select toggle Transparency, toggle Lighting, or ClipPlane to modify rendering options.

Transform coordinates to true spatial distances

  • 13

    In the SurfParam menu select item Transform to real space.

  • 14

    Enter the true/real spatial length of a voxel unit in meters.

  • 15

    In the SurfParam menu select item Save Surface Tesselation to save the result.

Cell track analysis

  • 16

    If you wish to use the protocol for surface reconstruction with subsequent cell track analysis, follow the extended protocol (Supplementary Manual 1).

TROUBLESHOOTING

Since the Voronoi mesh computation utilizes discrete voxel coordinates given by the image data, the precision of the Voronoi centroid computation decreases when a Voronoi element contains only relatively few voxels, i.e., the Voronoi resolution comes close to the image resolution. However, this is not a limitation of the reconstruction method, but related to the image quality and if necessary has to be overcome by an increase in image resolution. Low image resolutions mainly pose a problem in form of discrepancies between a higher in-plane and a lower out-of-plane (z-direction) resolution and visible ‘steps’ or ‘kinks’ may occur along the z direction. One intrinsic feature of the method presented here is that such z-direction ‘steps’ can be automatically interpolated. However, this only works as long as the z-steps are smaller than the reconstruction mesh element size (see Supp. Fig. 2, 3). If the Voronoi mesh elements have a higher resolution than the z-resolution of the image data, the z-steps are ‘precisely’ reconstructed (see Supp. Fig. 3 and 4), an unwanted phenomenon that is present in surface visualizations of microscopy data performed with most conventional software packages (e.g. Imaris®) that are widely used in biological microscopy that do not offer adaptive reconstructions. Thus, there is an optimum number of surface vertices that may correct limitations of microscopy data and more accurately represent the actual, real biological surface than higher-resolution surface meshes. In the method described here, this problem is automatically avoided when the number of vertices is adaptively adjusted (option B), but it has to be taken into account if the number of surface vertices used for the reconstruction is defined by the user (more is not necessarily better!). If adaptive reconstruction (option B) is used it has to be kept in mind that setting the quality parameter to high values (approaching the maximum 1.0) may in certain cases lead to very long processing times due to a large number of iterations. We therefore recommend starting with medium quality values.

TIMING

The computational time required to perform the task outlined above depends on the size of the microscopy data set, the intended reconstruction accuracy and the performance of the computer hardware. Typical times using recent computers for surface reconstruction are on the order of minutes.

ANTICIPATED RESULTS

Application of this protocol to segmented image data produces surface tesselations that consist of mesh points (‘vertices’) and a mesh topology (vertex connections, ‘edges’). The general features of the results that can be anticipated from the surface reconstruction protocol in general depend on the features of the true object, the image resolution with which the object is represented and the choice of the reconstruction parameters and their combination: First, it can be expected that with increasing number of Voronoi mesh elements the image data is more accurately reconstructed. We call this type of accuracy image-related accuracy and define it as the distance of the centroids of the triangular mesh that is formed by connected the Voronoi center points (the ‘dual’ mesh) from the voxel image surface. The second type of reconstruction quality is the accuracy with which the true object is represented by the surface tesselation, called ‘object-related accuracy’. While an increasing mesh resolution always leads to an increasing image-related accuracy, an increase in the number of mesh elements does not always produce better object-related accuracy and in such cases, a lower number of mesh elements might lead to a higher-object accuracy due to smoothing effects (see also ‘Troubleshooting’ and Supp. Fig. 3 and 4).

The iterative optimization process (both the homogenous and locally adaptive options) converges to optimal (high-quality) meshes (see Fig. 1), if the resolution of the voxel data is sufficiently fine in relation to the mesh element size (see also ‘Troubleshooting’). The effect of locally adaptive surface reconstruction on the results depends on the spatial properties of the image data. A spherical object will produce a result similar to that of homogeneous reconstruction, because the iterative refinement process depends on local membrane curvature, which is constant on a sphere. However, when objects have special spatial features (which are resolved in the image data), the local adaptivity produces inhomogeneously resolved surface meshes. An example for the latter case is the T cell surface reconstruction in which the membrane protrusion (shown in the lower right part of the cell in Fig. 5C and middle part of Fig. 5D) is automatically resolved by local adaptive mesh refinement.

The results of the surface reconstruction of the T cell alone, the T-B-cell conjugate and the germinal center border reconstruction are presented in Figures 4–6. Figure 4 (+ Supp. Video 1) and Fig. 5 (+ Supp. Video 2) offer a comparison between adaptive and homogeneous reconstruction and illustrate the optimization process. See also Supplementary Figures for additional examples. Supplementary Figure 5 shows example results obtained when two separate surfaces present in the same data set are reconstructed simultaneously. If regions exist where the distance between the surfaces is equal to or smaller than the reconstruction mesh spacing the separate surfaces might merge/attach to each other. This problem can be solved by increasing the mesh resolution or processing the surfaces separately. Exemplary results of the cell tracking analysis can be found in the supplementary material section ‘cell track analysis’, Figure 7 Supplementary Figure 6.

Figure 6.

Figure 6

Open in a new tab

Surface reconstruction of cell conjugates. A: Confocal microscopy data of a cognate T cell (green) forming a synapse with an antigen-presenting cell (blue). B: Surface reconstruction result (ratio out-of-plane/in-plane resolution 9:1).

Supplementary Material

Supplement

Figure 3.

Figure 3

Open in a new tab

Illustration of Voronoi surface elements. Reconstruction result after optimization (20 iterations) with adaptive vertex insertion (using T cell data shown in Figure 2). Because surfaces that are not perfect spheres cannot be approximated by 2-D planar polygonal Voronoi elements that have continuous transitions between neighboring cells. To achieve continuity at the element boundaries Voronoi elements are used that correspond to projections of the 2-D planar elements onto the voxel surface. These elements still fulfill the Voronoi criteria and are bended along the connections of neighboring Voronoi center points that form the edges of the dual surface triangulation. The Voronoi center points are located directly on the surface given by the voxel image data.

Acknowledgments

This research was supported by the Intramural Research Program of NIAID, NIH.

Footnotes

COMPETING FINANCIAL INTERESTS STATEMENT

The authors declare that they have no competing financial interests.

References

  • 1.Stoll S, Delon J, Brotz TM, Germain RN. Dynamic imaging of T cell-dendritic cell interactions in lymph nodes. Science (New York, N Y. 2002;296:1873–1876. doi: 10.1126/science.1071065. [DOI] [PubMed] [Google Scholar]
  • 2.Germain RN, et al. An extended vision for dynamic high-resolution intravital immune imaging. Seminars in immunology. 2005;17:431–441. doi: 10.1016/j.smim.2005.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Xu X, Meier-Schellersheim M, Yan J, Jin T. Locally controlled inhibitory mechanisms are involved in eukaryotic GPCR-mediated chemosensing. The Journal of cell biology. 2007;178:141–153. doi: 10.1083/jcb.200611096. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Couteau B, Payan Y, Lavallee S. The mesh-matching algorithm: an automatic 3D mesh generator for finite element structures. Journal of biomechanics. 2000;33:1005–1009. doi: 10.1016/s0021-9290(00)00055-5. [DOI] [PubMed] [Google Scholar]
  • 5.Lorensen WE, Cline EC. Marching Cubes: A high resolution 3D surface construction algorithm. Computer Graphics. 1987;21:163–169. [Google Scholar]
  • 6.Bootsma GJ, Brodland GW. Automated 3-D reconstruction of the surface of live early-stage amphibian embryos. IEEE transactions on bio-medical engineering. 2005;52:1407–1414. doi: 10.1109/TBME.2005.851500. [DOI] [PubMed] [Google Scholar]
  • 7.Yu X, et al. A novel biomedical meshing algorithm and evaluation based on revised Delaunay and Space Disassembling. Conf Proc IEEE Eng Med Biol Soc. 2007;2007:5091–5094. doi: 10.1109/IEMBS.2007.4353485. [DOI] [PubMed] [Google Scholar]
  • 8.Baker TJ. Mesh generation: Art or science? Progress in Aerospace Sciences. 2005;41:29–63. [Google Scholar]
  • 9.Qi H, Cannons JL, Klauschen F, Schwartzberg PL, Germain RN. SAP-controlled T–B cell interactions underlie germinal centre formation. Nature. 2008;455:764–769. doi: 10.1038/nature07345. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Voronoi G. Nouvelles applications des paramètres continus à la théorie des formes quadratiques. J reine angew Math. 1907;133:97–178. [Google Scholar]
  • 11.Lopreore CL, et al. Computational modeling of three-dimensional electrodiffusion in biological systems: application to the node of Ranvier. Biophysical journal. 2008;95:2624–2635. doi: 10.1529/biophysj.108.132167. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Dirichlet GL. Über die Reduktion der positiven quadratischen Formen mit drei unbestimmten ganzen Zahlen. J reine angew Math. 1850;40:209–227. [Google Scholar]
  • 13.Aurenhammer F. Voronoi Diagrams - A Survey of a Fundamental Geometric Data Structure. ACM Computing Surveys. 1991;23:345–405. [Google Scholar]
  • 14.Coggan JS, et al. Evidence for ectopic neurotransmission at a neuronal synapse. Science (New York, N Y. 2005;309:446–451. doi: 10.1126/science.1108239. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Kholodenko BN. Cell-signalling dynamics in time and space. Nature reviews. 2006;7:165–176. doi: 10.1038/nrm1838. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Lizana L, Konkoli Z, Bauer B, Jesorka A, Orwar O. Controlling chemistry by geometry in nanoscale systems. Annual review of physical chemistry. 2009;60:449–468. doi: 10.1146/annurev.physchem.040808.090255. [DOI] [PubMed] [Google Scholar]
  • 17.Neves SR, et al. Cell shape and negative links in regulatory motifs together control spatial information flow in signaling networks. Cell. 2008;133:666–680. doi: 10.1016/j.cell.2008.04.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Jones WP, Menzies KR. Analysis of the cell-centred finite volume method for the diffusion equation. Journal of Computational Physics. 2000;165:45–68. [Google Scholar]
  • 19.Germain RN, et al. Making friends in out-of-the-way places: how cells of the immune system get together and how they conduct their business as revealed by intravital imaging. Immunological reviews. 2008;221:163–181. doi: 10.1111/j.1600-065X.2008.00591.x. [DOI] [PubMed] [Google Scholar]
  • 20.Schwickert TA, et al. In vivo imaging of germinal centres reveals a dynamic open structure. Nature. 2007;446:83–87. doi: 10.1038/nature05573. [DOI] [PubMed] [Google Scholar]
  • 21.Allen CD, Okada T, Tang HL, Cyster JG. Imaging of germinal center selection events during affinity maturation. Science (New York, N Y. 2007;315:528–531. doi: 10.1126/science.1136736. [DOI] [PubMed] [Google Scholar]
  • 22.Hauser AE, et al. Definition of germinal-center B cell migration in vivo reveals predominant intrazonal circulation patterns. Immunity. 2007;26:655–667. doi: 10.1016/j.immuni.2007.04.008. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplement
NIHMS405718-supplement-Supplement.pdf (557.2KB, pdf)

RESOURCES

OSZAR »