Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2012 Aug 8.
Published in final edited form as: Brain Res. 2011 Jun 12;1405:77–84. doi: 10.1016/j.brainres.2011.05.066

Quantitative prediction of acute ischemic tissue fate using support vector machine

Shiliang Huang 1, Qiang Shen 1, Timothy Q Duong 1,2,3
PMCID: PMC3144979  NIHMSID: NIHMS311415  PMID: 21741624

Abstract

Accurate and quantitative prediction of ischemic tissue fate could improve clinical decision making in the clinical treatment of acute stroke. The goal of the present study is to explore the novel use of support vector machine (SVM) to predict infarct on a pixel-by-pixel basis using only acute cerebral blood flow (CBF), apparent diffusion coefficient (ADC) MRI data. The efficacy of SVM prediction model was tested on three stroke groups: 30-min, 60-min, and permanent middle-cerebral-artery occlusion (n=12 rats for each group). CBF, ADC and relaxation-time constant (T2) were acquired during the acute phase up to 3hrs and again at 24hrs. Infarct was predicted using only acute (30-min) stroke data. Receiver-operating characteristic (ROC) analysis was used to quantify prediction accuracy. The areas under the receiver-operating curves were 86±2.7%, 89±1.4%, and 93±0.8% using ADC+CBF data for the 30-min, 60-min and permanent middle cerebral artery occlusion (MCAO) group, respectively. Adding neighboring pixel information and spatial infarction incidence improved performance to 88±2.8%, 94±0.8%, and 97±0.9%, respectively. SVM prediction compares favorably to a previously published artificial neural network (ANN) prediction algorithm operated on the same data sets. SVM prediction model has the potential to provide quantitative frameworks to aid clinical decision-making in the treatment of acute stroke.

Keywords: SVM, ANN, fMRI, Perfusion-diffusion mismatch, Predictive model, DWI, PWI, ADC, CBF, Spatial infarction incidence

1. INTRODUCTION

Stroke is the fourth leading cause of death and the leading cause of long-term disability in the developed countries. Clinically, it is important not only to identify the extent of ischemic brain injury but also to render accurate and objective prediction of the likelihood of infarct on a pixel-by-pixel basis because such prognoses impact therapeutic regimen (Molina and Saver, 2005). Multimodal MRI of acute stroke provides clinically relevant data and predictive value to aid clinical decision-making and guide stroke therapy. In particular, the anatomical mismatch between perfusion and diffusion abnormality (Kidwell et al., 2003; Warach, 2003) approximates the potentially salvageable “ischemic penumbra” (Astrup et al., 1981a; Astrup et al., 1981b; Hossmann, 1994; Lo et al., 2005). Despite some shortcomings (Kidwell et al., 2003), perfusion-diffusion mismatch remains widely utilized to guide acute stroke treatment. By contrast, conventional T2-weighted MRI and computed tomography could not detect ischemic injury until at least 4–6 hours after stroke onset, coinciding with vasogenic edema at which point the tissue is likely already infracted.

Sophisticated algorithms have been developed to predict ischemic tissue fate and they included predictive models based on generalized linear model (Wu et al., 2001; Wu et al., 2007), probability-of-infarct (Shen et al., 2005b; Shen and Duong, 2008), and artificial neural network (ANN) (Huang et al., 2010). These predictive models provide statistical or probabilistic maps of infarct likelihood on a pixel-by-pixel basis utilizing only the acute MRI data. Performance analysis showed accurate prediction when compared with endpoint T2 MRI and/or histology.

Support vector machines (SVM), originated from the idea of structural risk minimization (Vapnik, 1995), have been used in a number of applications ranging from particle identification, face recognition and text categorization to engine knock detection, bioinformatics and database marketing (Campbell, 2000). Inputs are mapped onto a high dimensional feature space via kernel functions, and optimal hyperplanes are constructed to separate samples into different classes (Emblem et al., 2008; Zacharaki et al., 2009). SVM does not need an exact mathematical relation between input and output parameters. A unique advantage of SVM is that it is less prone to overfitting (Han and Kamber, 2006). SVM has been used in grading glioma based on contrast-enhanced perfusion MRI data (Wismuller et al., 2006) and classification of Alzheimer’s disease based on MRI data (Kemeny et al., 1999), and fMRI data analysis (Oczkowski and Barreca, 1997).

The goal of the present study is to explore the novel use of SVM to predict the likelihood of infarction on a pixel-by-pixel basis using only acute ADC and CBF data. The efficacy of the SVM prediction algorithm was tested on rat stroke models subjected to three different occlusion durations (30-min, 60-min and permanent middle cerebral artery occlusion (MCAO)). Predictions using ADC alone, CBF alone and ADC+CBF were evaluated. In addition, the effects of neighboring pixels and infarct incidence on prediction accuracy were also evaluated. Prediction accuracy was quantified using receiver-operating characteristic (ROC) analysis. Quantitative comparison of prediction accuracy was also made with the published ANN prediction results (Huang et al., 2010) operated on identical data sets.

2. RESULTS

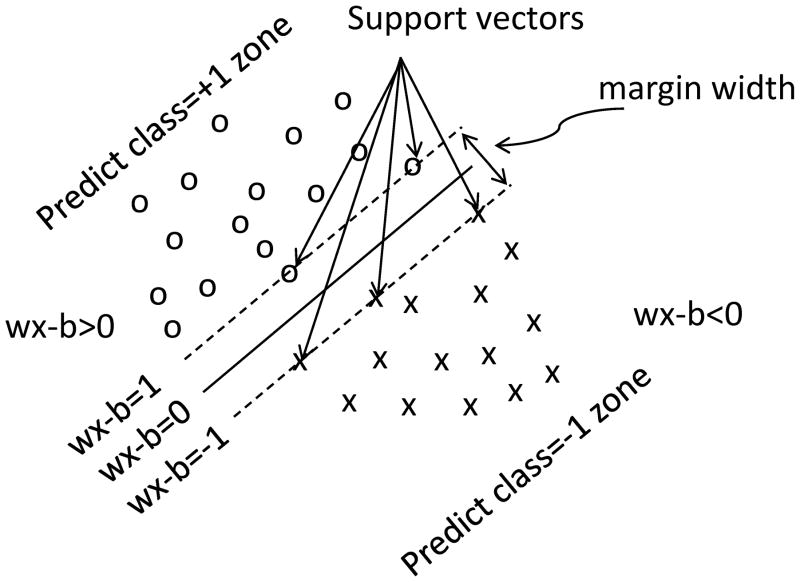
Figure 1 shows a schematic of the SVM model. SVM (Shawe-Taylor and Cristianini, 2000) is used to maximize the margin of the hyperplane dividing data into two groups. Figure 2 shows the normalized CBF and ADC scatterplot and the resulting hyperplane from the SVM algorithm. Representative data sets of the SVM predictions of subsequent infarction are shown in Figure 3 for the three experimental stroke groups using Training Method #1 where eleven animals were used as the “training” subject and the remaining one animal was used as “test” subjects. CBF alone, ADC alone, ADC+CBF, ADC+CBF+2D, ADC+CBF+3D, and ADC+CBF+3D + spatial information were evaluated. For references, ADC, CBF maps and ISODATA analysis of lesion volume based on ADC and T2 are also shown. ISODATA analysis of lesion volume was taken as the endpoint measure. SVM results were normalized from −1 to 1, where the more negative value indicated higher probability of infarct and the more positive value indicated higher probability of normal.

Figure 1.

Figure 1

Open in a new tab

A schematic demonstrating the concept of a linear support vector machine.

Figure 2.

Figure 2

Open in a new tab

A representative CBF-ADC scatterplot demonstrating the classification of two classes of pixels by SVM.

Figure 3.

Figure 3

Open in a new tab

Predicted infarct maps on a separate group of animals for permanent, 60-min, and 30-min MCAO using their own SVM training basis sets using Training Method #1. Multislice images are posterior to anterior slices from left to right. Predictions were made with CBF alone, ADC alone, ADC+CBF, ADC+CBF+2D adjacent pixels, ADC+CBF+3D adjacent pixels, ADC+CBF+3D adjacent pixels+ spatial information. For references, ADC, CBF maps and ISODATA analysis of endpoint lesion volume based on ADC and T2 are also shown. Note that only the representative 30-min data after MCAO was used in the prediction.

The major findings were as follows. For the permanent MCAO group, the predicted infarct maps showed generally good pixel-by-pixel correspondence with ISODATA cluster analysis of the end-point MRI data, with the exception of CBF data alone which poorly predicted infarct. With additional information (going from top to bottom), predictions were more accurate and more certain with respective to lesion location and volume. For the 60-min and the 30-min MCAO group, prediction with CBF alone was inaccurate and less certain compared to the permanent MCAO group. With additional information (from top to bottom), predictions were more accurate and more certain. Predicted maps were in general agreement with ISODATA analysis of lesion volume.

Figure 4 shows the areas under the ROC curves (AUC) for predictions using Training Method #1 where eleven animals were used as the “training” subject and the remaining one animal was used as “test” subjects. This was repeated for each animal in the same MCAO group. The major findings were: 1) CBF alone at 30 mins poorly predicted infarct across three experimental groups. 2) ADC alone adequately predicted infarct. 3) CBF+ADC improved prediction accuracy. 4) Addition of neighboring pixel information in 2D and 3D only slightly improved prediction accuracy. 5) Addition of infarction incidence further improved prediction slightly. 6) Finally, prediction was more accurate for the permanent MCAO group, followed by the 60-min and 30-min MCAO group.

Figure 4.

Figure 4

Open in a new tab

The areas under the ROC curves for three different occlusion durations: permanent, 30-min and 60-min MCAO using Training Method #1 where eleven animals were used as the “training” subject and the remaining one animal was used as “test” subjects.

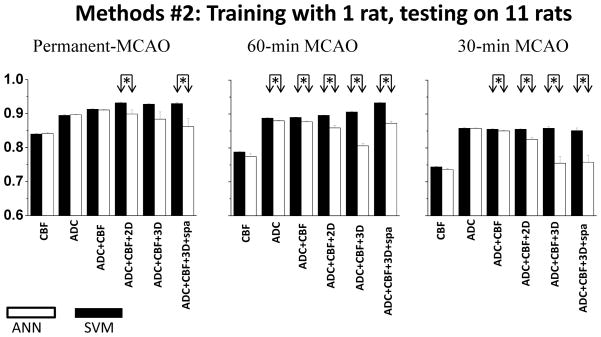
Figure 5 shows the AUC’s for predictions using Training Methods #2 where one animal was used as the “training” subject and the remaining eleven animals were used as “test” subjects. This was repeated for each animal in the same MCAO group. The observations were overall similar to those of Figure 4 except that AUCs were slightly smaller.

Figure 5.

Figure 5

Open in a new tab

The areas under ROC curves for three different occlusion durations: permanent, 30-min and 60-min MCAO using Training Methods #2 where one animal was used as the “training” subject and the remaining eleven animals were used as “test” subjects.

Comparisons were made with a previously published ANN prediction model (Huang et al., 2010). Figure 6 shows the results using Training Method #1, and Figure 7 shows the results using Training Methods #2. The statistical paired t-test of AUCs showed that SVM generally did better (yielding larger AUC) than ANN. This is particularly true for Training Methods #2.

Figure 6.

Figure 6

Open in a new tab

Comparison of SVM and ANN areas under ROC curves using Training Method #1 where eleven animals were used as the “training” subject and the remaining one animal was used as “test” subjects. The statistical paired t-test (P < 0.05) results were shown in this figure.

Figure 7.

Figure 7

Open in a new tab

Comparison of SVM and ANN areas under ROC curves using Training Methods #2 where one animal was used as the “training” subject and the remaining eleven animals were used as “test” subjects. The statistical paired t-test (P < 0.05) results were shown in this figure.

3. DISCUSSION

A flexible support vector machine algorithm was developed to predict ischemic tissue fate pixel-by-pixel based on multimodal MRI data of acute stroke. Predictions showed future likelihood of infarction on a pixel-by-pixel basis. Predictions were overall highly accurate. Accounting for neighboring pixels and infarction incidence improves prediction accuracy. SVM prediction compares favorably to ANN prediction, and especially where training sample size is small. SVM predictive algorithm has the potential to serve as promising metrics for diagnosis, prognosis and therapeutic evaluation of acute stroke, and other clinical applications.

SVM versus ANN prediction models

In SVM, AUCs were slightly larger using Training Method #1 than Training Method #2. This is likely because there was more information in 11 rats than that in 1 rat. Second, SVM outperformed ANN in both Method #1 and #2, which was particularly apparent in Method #2 where AUCs of ANN method decreased when additional information was added. This is likely because errors increased with more input parameters when the number of training data set was small.

The superior performance of SVM over ANN in our study is likely because: (1) SVM is based on the structural risk minimization principle which minimizes an upper bound for the generalization error rather than minimizing the training error. In contrast, ANN is based on the empirical risk minimization principle which may lead to poor generalization than SVM (Chen et al., 2005). (2) In SVM, finding the solution is equivalent to solving a linearly constrained quadratic programming problem, which leads to a global optimal solution. In contrast, ANN algorithm may not converge to global solution due to its theoretical weakness (Chen et al., 2005). (3) In choosing parameters, SVM is less complex than ANN. In contrast to neural networks SVMs automatically select their model size by selecting the support vectors. The parameters that must be determined in SVM are the RBF kernel parameter σ and the penalty factor C. However, in ANN, the number of hidden layers, number of hidden nodes, transfer functions and so on must be determined, which are comparatively more complex. Improper parameter selection might cause the over-fitting. (4) SVM provides accurate prediction with small sample size. This is because the decision function of SVM is only determined by supporting vectors. In general, the supporting vectors are only a part of all samples and other samples are not used in constructing the SVM model. Therefore the performance of SVM can still be acceptable even the sample size is small. In contrast, the decision function in ANN is determined by all training data sets. Thus, one rat data set (although there was many pixels) was apparent not enough to train ANN model, especially when there are more attributes (i.e., spatial information) in the training dataset. Finally, we note that while SVM has several advantages over ANN, it could not be generalized that SVM outperforms ANN. Comparisons of SVM and ANN have also been discussed elsewhere (Byvatov et al., 2003).

Comparison among predictive models

Wu et al. predicted infarction in normal and hypertensive stroke rats subjected to embolic clot occlusion with and without rt-PA treatment at 1 hr after stroke using voxel-based generalized linear model algorithm (Wu et al., 2007). They found that pre-treatment predicted outcome compared with post-treatment histology was highly accurate in saline-treated rats (92 ± 5%). Accuracy was significantly reduced in rt-PA treated animals (86 ± 8%). Animals that reperfused had significantly lower predicted infarction risk than nonreperfused animals, suggesting that tissue was more amenable to therapy. Shen et al. (Shen et al., 2005b; Shen and Duong, 2008) documented the probability-of-infarct profiles of stroke rats underwent different MCAO durations. Using only acute ADC and CBF data, pixel-by-pixel prediction was made and compared to endpoint T2 imaging and histology. The AUCs were 87±3%, 90±4%, and 93±3% using ADC+CBF for the 30-min, 60-min and permanent MCAO, respectively. Huang et al. (Huang et al., 2010) used ANN prediction algorithms and found that the AUCs were 86 ± 3%, 89 ± 2%, and 93 ± 1% using ADC+CBF for the 30-min, 60-min and permanent MCAO, respectively. Adding neighboring pixel information and spatial information improved performance measures over ADC and CBF alone for the 60-min and 30-min MCAO group (88 ± 3% and 94 ± 1%, respectively) but only slightly for the permanent MCAO group (94 ± 2%). These differences were expected because permanent MCAO was less variable and ADC and CBF alone sufficiently accounted for prediction accuracy. ANN method performed slightly better than the probability of infarct method (Shen and Duong, 2008) operated on the same data sets although there were some minor methodological differences in how training groups were assigned.

In this study using SVM prediction algorithms, the AUCs were 86 ± 2.7%, 89 ± 1.4%, and 93 ± 0.8% using ADC+CBF for the 30-min, 60-min and permanent MCAO, respectively. We found that CBF+ADC improved prediction accuracy. This is likely because CBF and ADC individually provided unique and relevant information. For example, in the presence of the perfusion and diffusion mismatch which would likely infract at later time points, neither ADC nor CBF data alone can capture such information. As such ADC would underestimate infarct volume while CBF overestimate infarct volume in this case. Moreover, perfusion deficit could overestimate final infarct volume if benign oligemia exists or reperfusion salvaged some tissue with initial perfusion deficit. Moreover, adding neighboring pixel information and spatial information markedly improved performance measures over ADC and CBF alone for the 60-min and 30-min MCAO group (94 ± 0.8% and 88 ± 2.8%, respectively) but again only slightly for permanent MCAO group (97 ± 0.9%).

The improvement in SVM results was apparent when compared with ANN operated on the same data sets. Differences in animal stroke models (embolic vs suture), anesthetics (halothane vs isoflurane), and inclusion of slightly different types of MRI data (dynamic susceptibility contrast vs arterial spin labeling CBF) preclude quantitative comparison with results reported by other research groups. Nonetheless, these quantitative prediction models (general linear model (Wu et al., 2007), probability-of-infarct method (Shen and Duong, 2008), ANN model (Huang et al., 2010) and SVM (this study)) based on acute MRI data were overall accurate and yielded comparable AUC’s on animal stroke models.

Surprisingly, AUCs improved only a few percents with additions of input parameters for prediction. This is because the performance measures based on the prediction of overall tissue fate have poor dynamic ranges. That is good performance is clustered at the very high percentage of sensitivity and specificity, and the AUCs are dominated by the fate of the “core” pixels. Partial area index to sample specific region of under the ROC curve region with a larger dynamic range has been proposed (Shen et al., 2005b; Shen and Duong, 2008). However, the choice of the ranges over which the area is integrated is subjective and such ranges could depend on diseases and/or disease stages. It has been shown previously that performance measures of individual tissue types could be assessed with improved AUC dynamic ranges, avoiding the aforementioned drawbacks (Shen et al., 2005b; Shen and Duong, 2008). Performance measures of individual tissue types could provide a more sensitive and appropriate assessment of the prediction accuracy compared to those of the overall tissue fates. This is currently under investigation.

This study established a novel SVM predictive algorithm and tested its efficacy on rat stroke models. Rats were subjected to three different occlusion durations to mimic the variable clinical conditions. SVM compares favorably to ANN in our study. SVM prediction model has the potential to provide quantitative and objective frameworks to aid clinical decision-making in the treatment of acute stroke, drug test, extend treatment window for stroke patients. Future studies will incorporate additional information such as fMRI, vascular permeability, oxygen consumption, oxygen extraction fraction, metabolic profile, and/or relaxation time measurements to improve prediction accuracy, and to apply to human stroke data.

4. EXPERIMENTAL PROCEDURE

Theory

SVM (Shawe-Taylor and Cristianini, 2000) is used to maximize the margin of the hyperplane dividing data into two groups. A hyperplane can be written as the set of points x satisfying, w · x − b = 0, where · denotes the dot product and the vector w is a normal vector perpendicular to the hyperplane. The parameter b||w|| determines the offset of the hyperplane from the origin along the normal vector w. w and b are chosen to maximize the margin (i.e., the distance between parallel hyperplanes as far apart as possible while still separating the data). These hyperplanes with the offset margins can be described by, w · x − b = 1, and w · x − b = −1.

“Soft margin” method is often used to choose a hyperplane that splits the examples as cleanly as possible, while still maximizing the distance to the nearest cleanly split examples by introducing the slack variables, ξi, which measure the degree of misclassification of the datum xi, yi (w · xi − b = ≥1 − ξi, where 1 ≤ ≤ n.

A loss function is added to the objective function and the optimization becomes a tradeoff between a large margin and a small error penalty. If the loss function is linear, the optimization problem becomes, minw,ξ{12||w||2+C∑i=1nξi}, subjected to yi (w · xi − b = ≥1 − ξi, where ξi ≥ 0, (for any i = 1,…,n), where C is the penalty factor to be chosen by the user, which controls the trade-off between training error and generalization ability.

SVM maps the samples x from the input space into the high dimensional feature space (inner product space) with a kernel function ϕ(x). The most commonly used kernel function is radial basis function (RBF) kernel, K(xi,xj)=exp(−||xi−xj||22σ2), which was used in this work.

Animal methods

The MRI stroke data used in this study were those from (Shen and Duong, 2008) which enabled comparison with a previously published ANN prediction method operated on identical data sets (Huang et al., 2010). A total of 36 Sprague-Dawley rats (300–350g) subjected to 30-min (n = 12), 60-min (n = 12) and permanent (n = 12) MCAO were utilized in this study. ADC and CBF were measured at 30, 60, 90, 120, and 180 mins after MCAO. For the 30-min and 60-min MCAO group, the 30-mins and 60-mins data, respectively, were acquired before reperfusion. Reperfusion was accomplished remotely without taking the animal out of the scanner. End-point T2 MRI was performed at 24 hrs post-occlusion.

Data analysis

To avoid susceptibility artifact from ear canal, five anterior slices were analyzed. Images were co-registered between acute phase and 24-hour data from the same animals and between animals (Liu et al., 2004; Schmidt et al., 2006; Shen et al., 2005a). ADC maps with intensity in unit of mm2/s (Meng et al., 2004; Shen et al., 2003) and CBF maps with intensity in units of mL/g/min were calculated (Duong et al., 2000). Image displays and overlays were performed on the STIMULATE software (University of Minnesota).

ISODATA cluster analysis

ISODATA was used to segment and exclude pixels of cerebrospinal fluid and the corpus callosum (Shen et al., 2004). With the remaining gray matter in the rat brain, ISODATA was used to identify pixels belonging to different tissue zones based on ADC and CBF data, and to determine final infarct volume based on end-point MRI data (Shen et al., 2004). Multiple clusters were resolved and identified as “normal”, “mismatch” and “ischemic core” from the ischemic right hemisphere at each acute time point (Shen et al., 2004). The final lesion was determined using ADC, and T2 maps at 24 hours post-occlusion, which had been previously correlated with histology (Shen et al., 2005b; Shen and Duong, 2008).

Spatial infarction incidence

To improve prediction accuracy, spatial infarction incidence maps were obtained by counting the frequency of infarction for each MCAO group. Spatial infarction incidence was referred as spatial frequency of infarct and described previously (Shen and Duong, 2008).

Support vector machine

SVM algorithms were developed in the Matlab environment utilizing the libsvm Toolbox. The penalty factor C and RBF kernel parameter σ were selected using grid search method. The optimal number of the penalty parameters C and the RBF kernel parameter σ were those that yielded the largest areas under the ROC curves.

Three experimental groups were analyzed: permanent, 60-min, and 30-min MCAO groups. The ADC and CBF data were normalized linearly to 0~1 before training the SVM model. SVM was trained and tested using leave-one-out cross-validation method (Cawley et al. 2003; Sharp et al., 2011; Gnatenko et al., 2010) and cycling for each individual animal in the same group. Two training methods were used. In Training Methods #1, 11 of the 12 animals were used as the “training” subjects and the remaining 1 animal was used as “test” subject. In Training Methods #2, 1 of the 12 animals was used as the “training” subject and the remaining 11 animals were used as “test” subjects.

Permanent MCAO SVM basis set was trained and applied to permanent MCAO animals for prediction using data at 30 mins after occlusion, 60-min MCAO SVM basis set was trained and applied to 60-min MCAO animals for prediction using data at 30 mins after occlusion, and 30-min MCAO SVM basis set was trained and applied to 30-min MCAO animals for prediction using data at 30 mins immediately before reperfusion. For each MCAO data set, training were performed for six conditions: 1) CBF alone, 2) ADC alone, 3) ADC+CBF, 4) ADC+CBF+2D adjacent pixels, 5) ADC+CBF+3D adjacent pixels, and 6) ADC+CBF+3D adjacent pixels+spatial information. For each MCAO data set, predictions were then made using only data obtained at 30 mins after stroke onset for each of the six conditions. Adjacent pixels referred to 8 and 26 immediate neighbor pixels in 2D and 3D, respectively (Huang et al., 2010). ADC and/or CBF of adjacent pixels were treated as independent inputs of SVM (for example, there were 18 inputs for the condition of ADC+CBF+2D, namely, that for each ADC pixel there were 8 neighbors, and for each CBF pixel there are 8 neighbors). Spatial information referred to the infarction incidence map described above. For display purpose, SVM prediction results were normalized to −1 ~ 1. The more negative value indicated higher probability of infarct and the more positive value indicated higher probability of normal.

ROC analysis, a more powerful way to quantify the prediction accuracy that accounts for false positive and false negative prediction, was performed to evaluate prediction accuracy as described previously (Shen et al., 2004). The areas under the ROC curves (AUC) were calculated for comparison. All group data were reported as mean ± SEM. Paired t-test was used for comparison of AUCs with P < 0.05 taken as statistical significance.

Comparison with a previously published ANN prediction model

SVM prediction results were compared with previously published ANN prediction results applied on the identical data sets (Huang et al., 2010).

Statistical Analysis

Two-way analysis of variance (ANOVA) with multiple-comparisons Tukey-Kramer’s correction was used for comparision among different conditions (Figures 4 and 5). The paired t-test was used for comparison between SVM and ANN model. P < 0.05 was taken to indicate statistical significance.

Highlights.

  • This study is to explore the novel use of support vector machine (SVM) to predict ischemic infarct.

  • The efficacy of SVM prediction model was tested on three stroke groups: 30-min, 60-min, and permanent stroke

  • Receiver-operating characteristic analysis showed accurate prediction.

  • Adding neighboring pixel information and spatial infarction incidence improved performance.

  • SVM has the potential to provide frameworks to aid clinical decision-making in the treatment of acute stroke.

Acknowledgments

This work was supported by the NIH (R01-NS45879) and the American Heart Association (EIA 0940104N, SDG-0430020N and SDG- 0830293N).

Abbreviation

SVM

support vector machine

ANN

artificial neural network

ADC

apparent diffusion coefficient

CBF

cerebral blood flow

ISODATA

iterative-self-organizing-data-analysis-algorithm

MCAO

middle cerebral artery occlusion

ROC

Receiver operating characteristic

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Astrup J, Sorensen PM, Sorensen HR. Oxygen and glucose consumption related to Na+/K+ transport in canine brain. Stroke. 1981a;12:726–730. doi: 10.1161/01.str.12.6.726. [DOI] [PubMed] [Google Scholar]
  2. Astrup J, Symon L, Siesjo BK. Thresholds in cerebral ischemia: the ischemic penumbra. Stroke. 1981b;12:723–725. doi: 10.1161/01.str.12.6.723. [DOI] [PubMed] [Google Scholar]
  3. Byvatov EUF, Sadowski J, Schneider G. Comparison of support vector machine and artificial neural network systems for drug/nondrug classification. J Chem Inf Comput Sci. 2003;43:1882–1889. doi: 10.1021/ci0341161. [DOI] [PubMed] [Google Scholar]
  4. Campbell C. Algorithmic approaches to training support vector machines: a survey. Proceedings of ESANN. 2000;2000:27–36. [Google Scholar]
  5. Cawley GC, Talbot NLC. Efficient leave-one-out cross-validation of kernel Fisher discriminant classifiers. Pattern Recognition. 2003;36:2585–2592. [Google Scholar]
  6. Chen WH, Hsu SH, Shen HP. Application of SVM and ANN for intrusion detection. Computers & Operations Research. 2005;32:2617–2634. [Google Scholar]
  7. Duong TQ, Silva AC, Lee S-P, Kim S-G. Functional MRI of calcium-dependent synaptic activity: cross correlation with CBF and BOLD measurements. Magn Reson Med. 2000;43:383–392. doi: 10.1002/(sici)1522-2594(200003)43:3<383::aid-mrm10>3.0.co;2-q. [DOI] [PubMed] [Google Scholar]
  8. Emblem KE, Zoellner FG, Tennoe B, Nedregaard B, Nome T, Due-Tonnessen P, Hald JK, Scheie D, Bjornerud A. Predictive modeling in glioma grading from MR perfusion images using support vector machines. Magn Reson Med. 2008;60:945–52. doi: 10.1002/mrm.21736. [DOI] [PubMed] [Google Scholar]
  9. Gnatenko DV, Zhu W, Xu X, Samuel ET, Monaghan M, Zarrabi MH, Kim C, Dhundale A, Bahou WF. Blood. 2010;115:7–14. doi: 10.1182/blood-2009-05-224477. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Han J, Kamber M. Data mining: concepts and techniques. Elsevier; San Francisco: 2006. [Google Scholar]
  11. Hossmann K-A. Viability Thresholds and the Penumbra of Focal Ischemia. Ann Neurol. 1994;36:557–565. doi: 10.1002/ana.410360404. [DOI] [PubMed] [Google Scholar]
  12. Huang S, Shen Q, Duong TQ. Artificial Neural-Network Prediction of Ischemic Tissue Fate in Acute Stroke Imaging. J Cereb Blood Flow Metab. 2010;30:1661–1670. doi: 10.1038/jcbfm.2010.56. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Kemeny V, Droste DW, Hermes S, Nabavi DG, Schulte-Altedorneburg G, Siebler M, Ringelstein EB. Automatic embolus detection by a neural network. Stroke. 1999;30:807–10. doi: 10.1161/01.str.30.4.807. [DOI] [PubMed] [Google Scholar]
  14. Kidwell CS, Alger JR, Saver JL. Beyond mismatch: evolving paradigms in imaging the ischemic penumbra with multimodal magnetic resonance imaging. Stroke. 2003;34:2729–35. doi: 10.1161/01.STR.0000097608.38779.CC. [DOI] [PubMed] [Google Scholar]
  15. Liu ZM, Schmidt KF, Sicard KM, Duong TQ. Imaging oxygen consumption in forepaw somatosensory stimulation in rats under isoflurane anesthesia. Magn Reson Med. 2004;52:277–285. doi: 10.1002/mrm.20148. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Lo EH, Moskowitz MA, Jacobs TP. Exciting, radical suicidal: how brain cell die after stroke. Stroke. 2005;36:189–192. doi: 10.1161/01.STR.0000153069.96296.fd. [DOI] [PubMed] [Google Scholar]
  17. Meng X, Fisher M, Shen Q, Sotak CH, Duong TQ. Characterizing the diffusion/perfusion mismatch in experimental focal cerebral ischemia. Ann Neurol. 2004;55:207–12. doi: 10.1002/ana.10803. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Molina CA, Saver JL. Extending reperfusion therapy for acute ischemic stroke: emerging pharmacological, mechanical, and imaging strategies. Stroke. 2005;36:2311–20. doi: 10.1161/01.STR.0000182100.65262.46. [DOI] [PubMed] [Google Scholar]
  19. Oczkowski WJ, Barreca S. Neural network modeling accurately predicts the functional outcome of stroke survivors with moderate disabilities. Arch Phys Med Rehabil. 1997;78:340–5. doi: 10.1016/s0003-9993(97)90222-7. [DOI] [PubMed] [Google Scholar]
  20. Schmidt KF, Febo M, Shen Q, Ferris CF, Stein E, Duong TQ. Hemodynamic and metabolic changes induced by Cocaine in anesthetized rat observed with multimodal functional. Psychopharmacology. 2006;185:479–486. doi: 10.1007/s00213-006-0319-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Sharp FR, Jickling GC, Stamova B, Tian Y, Zhan X, Liu D, Kuczynski B, Cox CD, Ander BP. Molecular markers and mechanisms of stroke: RNA studies of blood in animals and humans. J Cereb Blood Flow and Metab. 2011 doi: 10.1038/jcbfm.2011.45. [Epub ahead of print] [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Shawe-Taylor J, Cristianini N. Support Vector Machines and other kernel-based learning methods. Cambridge University Press; Cambridge, England: 2000. [Google Scholar]
  23. Shen Q, Meng X, Fisher M, Sotak CH, Duong TQ. Pixel-by-pixel spatiotemporal progression of focal ischemia derived using quantitative perfusion and diffusion imaging. J Cereb Blood Flow and Metab. 2003;23:1479–1488. doi: 10.1097/01.WCB.0000100064.36077.03. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Shen Q, Ren H, Bouley J, Fisher M, Duong TQ. Dynamic tracking of acute ischemic tissue fates using improved unsupervised ISODATA analysis of high-resolution quantitative perfusion and diffusion data. J Cereb Blood Flow Metab. 2004;24:887–897. doi: 10.1097/01.WCB.0000124321.60992.87. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Shen Q, Ren H, Cheng H, Fisher M, Duong TQ. Functional, perfusion and diffusion MRI of acute focal ischemic brain injury. J Cereb Blood Flow and Metab. 2005a;25:1265–1279. doi: 10.1038/sj.jcbfm.9600132. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Shen Q, Ren H, Fisher M, Duong TQ. Statistical Prediction of Tissue Fates in Acute Ischemic Brain Injury. J Cereb Blood Flow and Metab. 2005b;25:1336–1345. doi: 10.1038/sj.jcbfm.9600126. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Shen Q, Duong TQ. Quantitative Prediction of Ischemic Stroke Tissue Fate. NMR Biomed. 2008;21:839–848. doi: 10.1002/nbm.1264. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Vapnik V. The Nature of Statistical Learning Theory. Springer; New York: 1995. [Google Scholar]
  29. Warach S. Measurement of the ischemic penumbra with MRI: it's about time. Stroke. 2003;34:2533–2534. doi: 10.1161/01.STR.0000092395.19554.9A. [DOI] [PubMed] [Google Scholar]
  30. Wismuller A, Meyer-Baese A, Lange O, Reiser MF, Leinsinger G. Cluster analysis of dynamic cerebral contrast-enhanced perfusion MRI time-series. IEEE Trans Med Imaging. 2006;25:62–73. doi: 10.1109/TMI.2005.861002. [DOI] [PubMed] [Google Scholar]
  31. Wu O, Koroshetz WJ, Ostergard L, Buonanno FS, Copen W, Gonzales G, Rordorf G, Rosen BR, Schwamm LH, Weisskoff RM, Sorensen AG. Predicting tissue outcome in acute human cerebral ischemia using combined diffusion-and perfusion-weighted MR imaging. Stroke. 2001;32:933–942. doi: 10.1161/01.str.32.4.933. [DOI] [PubMed] [Google Scholar]
  32. Wu O, Sumii T, Asahi M, Sasamata M, Ostergaard L, Rosen BR, Lo EH, Dijkhuizen RM. Infarct prediction and treatment assessment with MRI-based algorithms in experimental stroke models. J Cereb Blood Flow and Metab. 2007;27:196–204. doi: 10.1038/sj.jcbfm.9600328. [DOI] [PubMed] [Google Scholar]
  33. Zacharaki EI, Wang S, Chawla S, Soo Yoo D, Wolf R, Melhem ER, Davatzikos C. Classification of brain tumor type and grade using MRI texture and shape in a machine learning scheme. Magn Reson Med. 2009;62:1609–18. doi: 10.1002/mrm.22147. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES

OSZAR »