Multi-Modal Image Set Registration and Atlas Formation

Peter Lorenzen; Marcel Prastawa; Brad Davis; Guido Gerig; Elizabeth Bullitt; Sarang Joshi

doi:10.1016/j.media.2005.03.002

. Author manuscript; available in PMC: 2008 Jun 18.

Published in final edited form as: Med Image Anal. 2006 Jun;10(3):440–451. doi: 10.1016/j.media.2005.03.002

Multi-Modal Image Set Registration and Atlas Formation

Peter Lorenzen ¹, Marcel Prastawa ¹, Brad Davis ¹, Guido Gerig ^1,², Elizabeth Bullitt ^1,^3,⁴, Sarang Joshi ^1,⁵

PMCID: PMC2430608 NIHMSID: NIHMS53782 PMID: 15919231

Abstract

In this paper, we present a Bayesian framework for both generating inter-subject large deformation transformations between two multi-modal image sets of the brain and for the forming of multi-class brain atlases. In this framework, the estimated transformations are generated using the maximal information about the underlying neuroanatomy present in each of the different modalities. This modality independent registration framework is achieved by jointly estimating the posterior probabilities associated with the multi-modal image sets and the high-dimensional registration transformations mapping the two subjects. To maximally use the information present in all the modalities for registration, Kullback-Leibler divergence between the estimated posteriors is minimized. Registration results for image sets composed of multi-modal MR images of healthy adult human brains are presented. Atlas formation results are presented for a population of five infant human brains.

Keywords: Multi-modal image set registration, atlas formation, inverse consistent registration, information theory, medical image analysis, computational anatomy

1 Introduction

With the increasing number of imaging techniques and imaging sensors, multi-modal image registration has become an active area of research in medical image analysis. An increasingly important area of medical image analysis is computational anatomy, the study of anatomical variation. Understanding anatomical variability requires robust high-dimensional image registration methods where the number of parameters used to describe the mappings between images is on the order of the number of voxels describing the space of the images.

Modern imaging techniques provide an array of imaging modalities which enable the acquisition of complementary information representing an underlying anatomy. Most image registration algorithms find a mapping between two scalar images. To utilize multi-modal images of a single anatomy, we define the notation of a multi-modal image set, Ī, as a collection of m co-registered multi-modal images, $\bar{I} (x) \in R^{m}$ . For example, Ī(x) might represent a CT image, a T1-weighted MR image, and a PET image of a single anatomy. We assume that the underlying neuroanatomy, represented in two acquired sets of multi-modal images, consists of a set, C, of separate anatomical structure classes, c_j. Throughout this paper, we assume that, for a given subject, the multi-modal images of that subject are co-registered.

Mutual information is typically used to register multi-modal images. High-dimensional image registration in the context of mutual information and other dissimilarity measures has been studied extensively. A thorough investigation of these dissimilarity measures in high-dimensional image registration is presented in [1]. A multi-modal free-form registration algorithm that matches voxel class labels, rather than intensities, via minimizing Kullback-Leibler divergence is presented in [2,3]. This method only finds correspondences between two scalar images. A method that minimizes Kullback-Leibler divergence between expected and observed joint class histograms is presented in [4]. This technique, however, estimates class labels as a preprocessing step and is used only for rigid registration between scalar images. The method presented in this paper is more general in that registration is performed on sets of images, of arbitrary number and is not constrained by an initial class labeling. Although inter-subject high-dimensional image registration has received much attention [5,6,7,8], to our knowledge, little attention has been given to the use of multi-modal image sets in image registration. The foundation for the work presented in this paper have been proposed in [9,10,11,12].

1.1 Model-Based Multi-Modal Image Set Registration

Across image sets, the number of constituent images may vary, thus registration based on an intensity similarity measure is not possible in this setting. While mutual information can be extended to multiple random variables, its extension to registration involving three or more images is problematic in that it requires maintaining an impractical number of histogram bins [13]. Given these difficulties we move to a model-based approach where the registration is performed using underlying anatomical structures. We incorporate these anatomical structures as a prior in a Bayesian framework.

This framework is based on the assumption that human brain anatomy consists of finitely enumerable structures such as grey matter, white matter, and cerebrospinal fluid. These structures present with varying radiometric intensity values across disparate image modalities. Given two multi-modal image sets, we capture the underlying structures by estimating, for each image set, the class posterior mass functions associated with each of the structures. These class posterior mass functions are then used to produce a mean posterior atlas by estimating high-dimensional diffeomorphic registration maps relating the coordinate spaces of the probability mass functions. The Kullback-Leibler divergence is used as a distance function on the space of probability mass functions to estimate the transformations. The use of the class posterior mass functions provides an image intensity independent approach to image registration.

1.2 Multi-Class Atlas Formation

An important problem in computational anatomy is the construction of an exemplar atlas from a population of medical images. This atlas represents the anatomical variation present in the population [14,15,16]. Many images are mapped into a common coordinate system to study intra-population variability and inter-population differences, to provide voxel-wise mapping of functional sites, and facilitate tissue and object segmentation via registration of anatomical labels. Common techniques for creating atlases often include the choice of a template image, which inherently produces a bias. Motivated by the atlas construction framework presented in [17], we propose the construction of an unbiased multi-class atlas from a population of anatomical class posteriors using large deformation diffeomorphic registration. When applied to two image sets, this atlas formation method yields inverse-consistent image registration.

1.3 Inverse Consistent Registration

Many registration algorithms are not inverse consistent since their dissimilarity metrics are computed in the coordinate system of either one of the images involved in the registration. This leads to order non-preservation of optimization energy cost functions. In traditional techniques for image registration solutions may be systematically biased with respect to expanding and contracting regions in the transformation [18]. Inverse consistent registration is desired when there is no preference, or believability, for one image over another. Existing methods for generating inverse consistent registration approximate inverse consistency by adding an inverse consistency penalty to the optimization cost function. The registration frameworks formulated in these methods are not intrinsically symmetric. A method for approaching this problem, involving an algorithm that estimates incremental transformations while approximating inverse consistency constraints on each incremental transformation, is presented in [19]. The approach presented in this paper is intrinsically inverse consistent as the registration problem is formulated symmetrically. Therefore, no correction penalty for consistency is required.

The remainder of this paper is organized as follows: Sections 2 and 3 cover the methodology of the multi-class atlas formation and the specification to two image set registration, results for these methods are presented in Sections 4 and 5 respectively, and finally, a discussion and conclusion are presented in Sections 6 and 7.

2 Methodology: Atlas Formation

In this section, we present the atlas formation framework and the motivation for the use of Kullback-Leibler divergence to drive the registration. We begin by describing the Bayesian framework for representing the anatomical class structures. The specification to image set registration involving two image sets is presented in Section 3.

2.1 Bayesian Framework

From a population of N multi-modal image sets ${{\bar{I}}_{i}}_{i = 1}^{N}$ , for each class c_j ∈ C, we first estimate the class posterior mass functions pⁱ(c_j(x)|Ī_i) for each image set i where c_j(x) is the class associated with the voxel at spatial position $x \in Ω \subset R^{3}$ . This method is independent of the number of images comprising each image set. These class posteriors are produced using the expectation maximization method described in [20,21]. Following [21], for each class c_j the associated data likelihood, p(Ī_i(x)|c_j(x), μ_j, Σ_j), is modeled as a normal distributions with mean, μ_j, and covariance, Σ_j.

2.2 Large Deformation Multi-Class Atlas Formation

We now consider the problem of estimating an atlas class posterior p̂ that is the best representative for a population of N class posteriors, ${p^{i}}_{i = 1}^{N}$ , representing the N individual image sets ${{\bar{I}}_{i}}_{i = 1}^{N}$ . The atlas p̂ is not a member of the {pⁱ}. To this end, we consider the problem of constructing a mapping between p̂ and each class posterior in the set {pⁱ}. That is, we estimate the mappings h_i: Ω → Ω_i where $Ω \subset R^{3}$ and $Ω_{i} \subset R^{3}$ are the coordinate systems of the class posteriors p̂ and pⁱ respectively. The coordinate system Ω is chosen to be independent of the individual population class posterior coordinate systems, Ω_i. This framework is depicted in Figure 1.

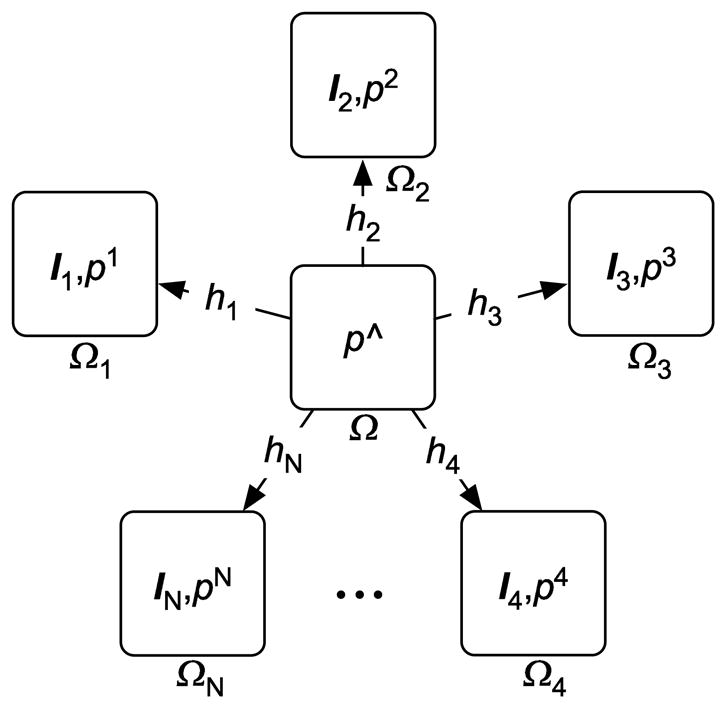
Unbiased atlas constructed as the intrinsic mean of a population of class posteriors.

We seek the representative atlas class posterior p̂ that requires the minimum amount of energy to deform into every population class posterior pⁱ. More precisely, given a transformation group S with associated metric $D : S^{2} \to R$ , along with a probability density dissimilarity measure E(p, q), we wish to find the class posterior density p̂ such that

{{\hat{h}}_{i}, \hat{p}} = \underset{h_{i} \in S, p}{arg min} \sum_{i = 1}^{N} E (p^{i} \circ h_{i}, p) + D^{2} (e, h_{i})

(1)

where e is the identity transformation.

In this paper, we focus on the infinite dimensional group of diffeomorphisms $H$ where we apply the theory of large deformation diffeomorphisms [6,22] to generate deformations h_i that are solutions to the Lagrangian ODEs $\frac{d}{d t} h_{i} (x, t) = v_{i} (h (x, t), t), t \in [0, 1]$ . The transformations h_i are generated by integrating velocity fields forward in time and $h_{i}^{- 1}$ are generated by integrating velocity fields backward in time. The relationship between spatial locality, velocity fields, and time is shown in Figure 2. The spatial location y is described in terms of the forward integration of the velocity field υ starting from spatial location x, that is, $y = h (x, 1) = x + \int_{0}^{1} v (h (x, τ), τ) d τ$ . Similarly, x can be described in terms of integrating the reverse velocity field υ̃ starting at y, that is, $x = φ (y, 1) = y + \int_{0}^{1} \tilde{v} (φ (y, τ), τ) d τ$ . From this figure we note that υ(h(x, t), t) = −υ̃(φ(y, 1−t),1−t) and, hence, ||Lυ(x), t)||² = ||Lυ̃(y), 1−t)||² where L = α∇² + β∇·∇ + γ is the Navier-Stokes operator.

We induce a metric on the space of diffeomorphisms by using a Sobolev norm (a norm that involves derivatives of a function) via the partial differential operator L on the velocity fields υ. Let h be a diffeomorphism isotopic to the identity transformation e. We define the squared distance D²(e, h) as

D^{2} (e, h) = min_{v} \int_{0}^{1} \int_{Ω} ∥ L v (x, t) ∥^{2} dxdt

subject to

h (x) = x + \int_{0}^{1} v (h (x, t), t) d t .

The distance between any two diffeomorphisms is defined by

D (h_{1}, h_{2}) = D (e, h_{1}^{- 1} \circ h_{2}) .

The construction of h and h⁻¹, as well as the properties of D, are described in [17].

Having defined a metric on the space of diffeomorphism and a regularization operator L, the energy minimization problem (Equation 1) is formulated as

{{\hat{h}}_{i}, \hat{p}} = \underset{h_{i}, p}{arg min} \sum_{i = 1}^{N} E (p^{i} \circ h_{i}, p) + \int_{0}^{1} \int_{Ω} ∥ L v_{i} (x, t) ∥^{2} dxdt

(2)

subject to

h_{i} (x) = x + \int_{0}^{1} v_{i} (h_{i} (x, t), t) d t .

2.3 Kullback-Leibler Divergence

As a measure of dissimilarity between two class posteriors, we use Kullback-Leibler divergence (relative entropy).

Definition 1

Let p and q be probability mass functions on a set C. The Kullback-Leibler divergence [23] between p and q is

D_{K L} (p ∥ q) = \sum_{c_{j} \in C} p (c_{j}) log \frac{p (c_{j})}{q (c_{j})} .

The Information Inequality theorem provides the basic properties of D_KL(p||q):

Theorem: (Information Inequality): Let p(c_j), q(c_j) be two probability mass functions on the set C. Then D_KL(p||q) ≥ 0 with equality if and only if p(c_j) = q(c_j) for all c_j∈C.

Proof: an application of Jensen’s inequality, see [24].

In our setting, we use the Kullback-Leibler divergence as a measure of dissimilarity between the two probability mass functions p^Ω and pⁱ at spatial location x ∈ Ω,

D_{K L} (p^{Ω} (x) ∥ p^{i} (x)) = \sum_{c_{j} \in C} p^{Ω} (c_{j} (x)) log \frac{p^{Ω} (c_{j} (x))}{p^{i} (c_{j} (x))} .

From an information theoretic viewpoint [24], this dissimilarity can be interpreted as the inefficiency of assuming that pⁱ(x) is true when p^Ω(x) is true. That is, if we have a model expressed as a probability mass function pⁱ(x), we can then measure how far an observation, also expressed as a probability mass function, p^Ω(x), deviates from pⁱ(x) using Kullback-Leibler divergence.

2.3.1 Bayes Probability of Error

The use of Kullback-Leibler divergence as a distance function is appropriate in this setting as it provides a lower bound on the Bayes probability of error, P(error), between two probability mass functions. Specifically, reducing D_KL(·) increases a lower bound on P(error).

Motivated by [25], we can consider the two-hypothesis decision-theory problem of classifying an observation as coming from one of two possible hypotheses H₁, the average class posterior p^Ω(x), and H₂, the class posterior of one of the deformed image sets Ī_i, pⁱ(h_i(x)). Let q(H₁) and q(H₂) denote the a prior probabilities on the two hypotheses, and let q(c|H₁) and q(c|H₂) denote the class conditional probability density functions given the true hypotheses. For an observed class structure, c, (e.g., white matter), the posterior probability of H_k is

q (H_{k} ∣ c) = \frac{q (c ∣ H_{k}) q (H_{k})}{q (c ∣ H_{1}) q (H_{1}) + q (c ∣ H_{2}) q (H_{2})}

for k = 1,2. To minimize the probability of error, choose the hypothesis with the larger posterior probability. Therefore,

\begin{array}{l} P (error ∣ c) = min {\frac{q (c ∣ H_{1}) q (H_{1})}{q (c ∣ H_{1}) q (H_{1}) + q (c ∣ H_{2}) q (H_{2})}, \\ \frac{q (c ∣ H_{2}) q (H_{2})}{q (c ∣ H_{1}) q (H_{1}) + q (c ∣ H_{2}) q (H_{2})}} \end{array}

and, hence,

\begin{array}{l} P (error) = E_{c} [P (error ∣ c)] \\ = \sum_{c \in C} min {q (c ∣ H_{1}) q (H_{1}), q (c ∣ H_{2}) q (H_{2})} d c \end{array}

where $E_{c}$ denotes the expectation with respect to c. The probability of error is graphically depicted in Figure 3. In our registration problem we want to maximize P(error). That is, the closer we can make these posterior distributions, the larger will be the probability of mistaking one for the other, an increase in indistinguishability.

Let q(H₁) and q(H₂) represent the a priori probabilities of hypothesis H₁ and H₂ being true respectively and q(c|H₁] and q(c|H₂) be the hypothesis-conditioned likelihoods for class c. In the context of neuroanatomical matching, c could be grey matter, white matter, or cerebrospinal fluid. The densities q(c|H₁)q(H₁) and q(c|H₂)q(H₂) correspond to the atlas class posterior p^Ω(x) and the class posterior of the deformed image set *Ī_i*, pⁱ at a given spatial location x.

In practice, real distributions are not known so the P(error) can not be directly computed. Given this reality, we look for a lower-bound on P(error) which is maximized when D_KL(·) is minimized.

2.3.2 Bounds on P(error) for Our Two-Hypothesis Problem

One of the first divergence measures involving density ratios is the Jeffreys divergence [26],

J (q_{1} ∥ q_{2}) = D_{K L} (q_{1} ∥ q_{2}) + D_{K L} (q_{2} ∥ q_{1}) .

As will be described in Section 3.2, this symmetric form of Kullback-Leibler divergence will be used as the distance measure to drive the registration. Using inequalities derived in [27] a lower bound on P(error) in terms of J(q₁||q₂) is presented in [25,28], $\frac{1}{4} e^{- \frac{J}{2}} \leq P (error)$ . Thus, a reduction in D_KL(·) leads to an increase in the lower bound of P(error). It should be noted, that while we have defined Jeffreys divergence in terms of symmetric Kullback-Leibler divergence, Sir Harold Jeffreys published his divergence measure in 1946 [26] while Solomon Kullback and Richard Leibler published theirs in 1951 [23].

2.4 Registration

Under the Kullback-Leibler divergence, Section 2.3, measure the atlas estimation problem in Equation 2 becomes

{{\hat{h}}_{i}, \hat{p}} = \underset{h_{i}, p}{arg min} \sum_{i = 1}^{N} \int_{Ω} D_{K L} (p (x) ∥ p^{i} (h_{i} (x))) d x + \int_{0}^{1} \int_{Ω} ∥ L v_{i} (x, t) ∥^{2} dxdt .

(3)

This minimization problem can be simplified by noticing that for fixed transformations h_i the p̂ that minimizes Equation 3 is given by normalized geometric mean of the deformed class posteriors, pⁱ(h_i(x)),

\hat{p} (c_{j} (x)) = \frac{{(\prod_{i = 1}^{N} p^{i} (h_{i} (c_{j} (x))))}^{\frac{1}{N}}}{\sum_{c_{k} \in C} {(\prod_{i = 1}^{N} p^{i} (h_{i} (c_{k} (x))))}^{\frac{1}{N}}} .

(4)

Combining Equations 3 and 4 results in the following minimization problem

{\hat{h}}_{i} = \underset{h_{i}}{arg min} \sum_{i = 1}^{N} \int_{Ω} D_{K L} (\hat{p} (x) ∥ p^{i} (h_{i} (x))) d x + \int_{0}^{1} \int_{Ω} ∥ L v_{i} (x, t) ∥^{2} dxdt .

(5)

Note that the solution to this minimization problem is independent of the ordering of the N image sets and increases linearly as image sets are added, thus, making the algorithm scalable.

2.5 Implementation

Following Christensen’s greedy algorithm for propagating templates [29], we use the algorithm for propagating templates. In the atlas formation setting, the velocity $v_{i}^{n}$ for each iteration n is computed as follows. First, compute the updated atlas estimate (i.e. the normalized geometric mean)

{\hat{p}}^{n} (c_{j} (x)) = \frac{{(\prod_{i = 1}^{N} p^{i} (h_{i}^{n} (c_{j} (x))))}^{\frac{1}{N}}}{\sum_{c_{k} \in C} {(\prod_{i = 1}^{N} p^{i} (h_{i}^{n} (c_{k} (x))))}^{\frac{1}{N}}} .

for each class component c_j. Next, using the second order approximation to Kullback-Leibler divergence, we define the body force functions

F_{i}^{n} (x) = \sum_{c_{k} \in C} [\frac{p^{i} (h_{i} (c_{k} (x)))}{\hat{p} (c_{k} (x))} - 2] \nabla p^{i} |_{c_{k} (h_{i} (x))}^{T} .

This is the variation of the class posterior dissimilarity term in Equation 5 with respect to the transformation h_i. The velocity field $v_{i}^{n}$ is computed at each iteration by applying the inverse of the differential operator L to the body force function, i.e. $v_{i}^{n} (x) = L^{- 1} F_{i}^{n} (x)$ . This computation is performed in the Fourier domain [30].

The forward and backward integration is described as follows. At time t the transformations h_i are described as

\begin{array}{l} h_{i} (x, t + δ) = h_{i} (x, t) + \int_{t}^{t + δ} v_{i} (h_{i} (x, τ), τ) d τ \\ \approx h_{i} (x, t) + δ v_{i} (h_{i} (x, t), t) \end{array}

for small δ. At iteration k of the algorithm, the transformations h_{1,2} become the telescoping compositions $h_{i} = h_{i}^{1} \circ h_{i}^{2} \circ \dots \circ h_{i}^{k}$ . At time t the inverse transformations $h_{i}^{- 1}$ are described as

\begin{array}{l} h_{i}^{- 1} (y, t) = h_{i}^{- 1} (y - \int_{t}^{t - δ} v_{i} (y, τ) d τ, t - δ) \\ \approx h_{i}^{- 1} (y - δ v_{i} (y, t), t - δ) \end{array}

for small δ. At iteration k of the algorithm, the transformations $h_{i}^{- 1}$ become the telescoping compositions $h_{i}^{- 1} = h_{i}^{- 1, k} \circ h_{i}^{- 1, k - 1} \circ \dots \circ h_{i}^{- 1, 1}$ .

3 Methodology: Image Set Registration

In this section, we present the specification of the atlas formation problem of Section 2 to the problem of image set registration involving two image sets. That is, we consider the problem of finding a mapping between image sets Ī₁ and Ī₂ (Figure 4). That is, we would like to find the mappings f: Ω₁ → Ω₂ and g: Ω₂ → Ω₁ where Ω₁ and Ω₂ are the coordinate systems of image sets Ī₁ and Ī₂ respectively. Again, we introduce a new coordinate system Ω, independent of Ω₁ and Ω₂. Let transformations h₁ and h₂ map Ω to Ω₁ and Ω₂ respectively. By construction, $f = h_{2} \circ h_{1}^{- 1}$ and $g = h_{1} \circ h_{2}^{- 1}$ . This registration method is inverse consistent as f∘g = g∘f = Id, the identity map.

Registration of image sets Ī₁ and Ī₂ through the unbiased coordinate space Ω.

3.1 Bayesian Framework

From the multi-modal images Ī₁ and Ī₂, for each class c_j ∈ C we jointly estimate the posterior mass functions p¹(x) = p(c_j(h₁(x))|Ī₁) and p²(x) = p(c_j(h₂(x))|Ī₂) along with the registration maps h₁(x) and h₂(x), that map the independent coordinate space $Ω \subset R^{3}$ , into the space of subject one, $Ω_{1} \subset R^{3}$ , and subject two, $Ω_{2} \subset R^{3}$ , respectively. This method is independent of the choice of the number of images comprising each image set. Optimal inter-subject multi-modal image registration is estimated by an alternating iterative algorithm which is motivated by an expectation maximization method used in [20,21]. Our algorithm interleaves the estimation of the posteriors associated with subjects one and two and the estimation of the registration maps h₁: Ω → Ω₁ and h₂: Ω → Ω₂.

As in Section 2.1, for each class c_j the associated data likelihoods, p(Ī{1,2}(x)|c_j(x), μ_j, Σ_j), are modeled as a normal distributions with means, μ_j, and covariances, Σ_j. Given the transformations h₁ and h₂ and the current estimates μ_j and Σ_j for both image sets, the posteriors of subjects one and two are associated with the independent coordinate probability mass function p^Ω by using Bayes’s Rule with p^Ω as the prior for both posteriors p^l(x) and p²(x). Having defined the posteriors, the parameters μ_j and Σ_j are updated by their expected values. We are currently investigating the use of kernel density estimation as a replacement for the Gaussian models as described in [31].

Given the transformations h₁ and h₂ and the current estimates μ_j and Σ_j for both image sets, the posteriors of the two subjects are associated with the independent coordinate probability mass function p^Ω by using Bayes’s Rule with p^Ω as the prior for both posteriors p^l(x) and p²(x). Having defined the posteriors, the parameters μ_j and Σ_j are updated by their expected values. We are currently investigating the use of kernel density estimation as a replacement for the Gaussian models as described in [31].

3.2 Registration

At a given point x ∈ Ω the dissimilarity between image sets Ī₁(x) and Ī₂(x) is measured by the dissimilarity between the posterior mass functions modeling them, p¹(x) and p²(x). As we have seen in Section 2.3.2, minimizing the Jeffrey’s divergence between two probability mass functions increases the lower bound on the Bayes’ probability of error in the two-hypothesis decision problem, and, thus, renders the probability mass functions more indistinguishable. That is, brings them closer together. The following distance is used to drive the registration

D (p^{1} (x), p^{2} (x)) = \underset{p^{Ω} (x)}{arg min} [D_{K L} (p^{Ω} (x) ∥ p^{1} (x)) + D_{K L} (p^{Ω} (x) ∥ p^{2} (x))] .

(6)

From Equation 6, D(p¹(x), p²(x)) = D(p²(x), p¹(x)). For known transformations h₁ and h₂ the probability mass function in the independent coordinate system, p^Ω(x), that minimizes the distance above is the normalized geometric mean

p^{Ω} (c_{j} (x)) = \frac{{(p^{1} (c_{j} (x)) p^{2} (c_{j} (x)))}^{\frac{1}{2}}}{\sum_{c_{k} \in C} {(p^{1} (c_{k} (x)) p^{2} (c_{k} (x)))}^{\frac{1}{2}}} .

Thus, the dissimilarity metric can be expressed wholly in terms not involving the independent coordinate system. After substituting this value for p^Ω into Equation 6 we obtain the following distance at position x ∈ Ω

D (p^{1} (x), p^{2} (x)) = - 2 log \sum_{c_{j} \in C} {(p^{1} (h_{1} (c_{j} (x)) ∣ {\bar{I}}_{1}) p^{2} (h_{2} (c_{j} (x)) ∣ {\bar{I}}_{2}))}^{\frac{1}{2}} .

With this result we re-write the minimization problem stated in Equation 1 as follows

\begin{array}{l} {\hat{v}}_{1}, {\hat{v}}_{2} = \underset{v_{1}, v_{2}}{arg min} \int_{Ω} log \sum_{c_{j} \in C} {(p^{1} (h_{1} (c_{j} (x)) ∣ {\bar{I}}_{1}) p^{2} (h_{2} (c_{j} (x)) ∣ {\bar{I}}_{2}))}^{\frac{1}{2}} d x \\ + \int_{0}^{1} \int_{Ω} ∥ L v_{1} (x) ∥^{2} dxdt + \int_{0}^{1} \int_{Ω} ∥ L v_{2} (x) ∥^{2} dxdt . \end{array}

3.3 Implementation

As described in Section 2.5, we compute the variation for h₁ of the average D(p¹(x), p²(x)) term

\frac{\partial}{\partial h_{1}} \frac{1}{∣ Ω ∣} \int_{Ω} D (p^{1} (x), p^{2} (x)) d x = - \frac{1}{∣ Ω ∣} \int_{Ω} \frac{\sum_{c_{j} \in C} {(\frac{p^{2} (c_{j} (x))}{p^{1} (c_{j} (x))})}^{\frac{1}{2}} \nabla p^{1} ∣_{c_{j} (h_{1} (x))}^{T}}{\sum_{c_{k} \in C} {(p^{1} (c_{k} (x)) p^{2} (c_{k} (x)))}^{\frac{1}{2}}} d x .

In a similar manner the variation for h₂ is computed. The velocity fields υ_{1,2} at each iteration are updated by solving the partial differential equation,

L v_{{1, 2}} (x, t) = \frac{\partial}{\partial h_{{1, 2}}} \frac{1}{∣ Ω ∣} \int_{Ω} D (p^{1} (x), p^{2} (x)) d x .

4 Results: Atlas Formation

To evaluate the performance of the atlas formation method, we applied the algorithm to a set of five class posterior mass functions that where derived from a population of T1-weighted, T2-weighted, and proton density 3D MR images of brains of health two year old children, acquired at UNC Chapel Hill, using an expectation maximization segmentation method [21,32]. As a preprocessing step, these images were aligned using affine registration. An axial slice from each derived class posterior mass function is shown in Figure 5. There is noticeable variation between these anatomies, especially in the ventricular region.

Five class posteriors (columns) each with four classes (rows). These images clearly show the large inter-subject variability, especially in the ventricular system.

Figure 6 shows the normalized geometric mean of the five class posterior mass functions and the final estimate of the atlas. The normalized geometric mean is blurry since it is an “average” of the varying individual neuroanatomies. Ghosting is evident around the lateral ventricles and near the boundary of the brain. In the final estimate of the atlas these variations have been accommodated by the high-dimensional registration.

The top row shows the normalized geometric mean class posterior density following an affine registration of all five subjects. The bottom row represents the estimated atlas after the final iteration of the algorithm.

5 Results: Image Set Registration

To evaluate the image set registration method, we defined a collection of image sets of increasing complexity. For each image subject, the image sets were created using 3D scalar images from a population of four imaging modalities: MRA, T1-FLASH MR, T1-MPRAGE MR, and T2 MR. The composition of these image sets is described in Section 5.2.1. The individual MR images were acquired at UNC Chapel Hill using a Siemens head-only 3Tesla system (Allegra, Siemens Medical Systems Inc.) and a Siemens 1.5Tesla system (Sonata, Siemens Medical Systems Inc.) with a head coil. Imaging parameters, TR/TE/TH/in-plane resolution, for the T1 and T2 image acquisitions are as follows, 15msec/7msec/lmm/l × 1 mm² and 7730msec/80msec/lmm/1 × 1 mm² respectively. Additionally, a 3D time-of-flight MRA sequence was acquired. Velocity compensation along both frequency and phase encoding direction was used to maximize signal de-phasing induced by the flowing spins. A magnetization transfer pulse was used to suppress signal from brain parenchyma while maintaining signal from flowing spins. The acquired spatial resolution for the MRA images was 0.5134 × 0.5134 × 0.78 mm³ and 1 × 1 × 1 mm³ for the T1 and T2 images. The MRA images were resampled to the 1 × 1 × 1 mm³ resolution.

5.1 Data Preprocessing

The tissue exterior to the brain was removed using a mask generated by a brain segmentation tool based on the method described in [31]. The geometric prior used to initialize the algorithm was also produced using this tool. Mid-axial, mid-coronal, and mid-sagittal slice views for subjects one and two are presented in Figures 7 and 8 respectively. These four modalities provide complementary information. For example, the T1-FLASH and T1-MPRAGE images have contrast differences and the MRA images exhibit missing information due to grey matter/white matter wash out and axial slab effect. In these examples, the set of structural classes is taken to be

C = {c₁ = grey matter, c₂ = white matter, c₃ = cerebrospinal fluid, c₄ = other}.

5.2 Registration Experiments

To evaluate this image set registration framework, we first estimated transformations, f₁ and g₁, relating the coordinate spaces of subject one and subject two by applying our method to a mono-modal registration. These two transformations were then used as “ground truth” for the purpose of evaluating an increasingly complex collection of image set registrations. Quantitative analysis of these results involves computing the inverse-consistency error.

We performed the following eight registration experiments

Mono-modal/Mono-modal (common): Ī₁ = T1-FLASH of subject one and Ī₂ =T1-FLASH of subject two.
Mono-modal/Mono-modal (mutually exclusive): Ī₁ = T1-FLASH of subject one and Ī₂ =T2 of the subject two.
Bi-modal/Bi-modal (fully common): Ī₁ = T1-FLASH and T2 of subject one and Ī₂ = T1-FLASH and T2 of subject two.
Bi-modal/Bi-modal (single common): Ī₁ = T1-FLASH and T2 of subject one and Ī₂ = T1-MPRAGE and T2 of subject two.
Bi-modal/Bi-modal (mutually exclusive): Ī₁ = T1-FLASH and T2 of subject one and Ī₂ = T1-MPRAGE and MRA of subject two.
Bi-modal/Mono-modal (mutually exclusive): Ī₁ = T1-FLASH and T2 of subject one and Ī₂ = MRA of subject two.
Tri-modal/Tri-modal (fully common): Ī₁ = T1-FLASH, T1-MPRAGE, and T2 of subject one and Ī₂ = T1-FLASH, T1-MPRAGE, and T2 of subject two.
Quad-modal/Quad-modal (full common): Ī₁ = T1-FLASH, T1-MPRAGE, T2, and MRA of subject one and Ī₂ = T1-FLASH, T1-MPRAGE, T2, and MRA of subject two.

From each of these experiments, transformations f_i and g_i are obtained. The first experiment provides the “ground truth” transformations, f₁ and g₂. The T1-FLASH modality was chosen for the first experiment due to its relatively good white matter/grey matter contrast.

5.2.2 Bi-Modal/Bi-Modal (mutually exclusive) Registration

For the purposes of brevity we present qualitative results for the most interesting of these experiments, the bi-modal/bi-modal mutually exclusive registration. In this experiment, Ī₁ represents the T1-FLASH and T2 images acquired from subject one and Ī₂ represents the T1-MPRAGE and MRA images acquired from subject two. The estimated forward, f, and backward, g, transformation are depicted in Figures 9 and 10 respectively.

The top row shows mid-axial, mid-coronal, and mid-sagittal views of image set Ī₁(x) and the bottom row shows the same views for the deformed image set Ī₂(f(x)).

The top row shows mid-axial, mid-coronal, and mid-sagittal views of image set Ī₂(x) and he bottom row shows the same views for the deformed image set Ī₁(g(x)).

5.2.3 Inverse-Consistency

We used the L₂ difference norm, ||f₁(g_i(x))−x||₂, to evaluate inverse-consistency between each experiment, i, and the first experiment for each spatial location x ∈ Ω. For numerical stability these inverse-consistency errors were computed via telescoping compositions as described in Section 2.5. Over all eight experiments, the maximum computed inverse consistency error was 3.12 × 10⁻⁴ voxels with an average of 5.04 × 10⁻⁵ voxels.

6 Discussion

The multi-modal image set registration as presented here might be potentially significant in various applications which rely on the measurement of image sets. For example, multi-modal imaging is standard in the imaging of pathologies such as tumors and lesions. Registration between images presenting pathology and images of healthy subjects is a challenging task since space-occupying lesions have to be treated differently from infiltrating lesions. Specifically, the registration needs to accommodate both local spatial deformation and local change of image intensity. Existing registration method involving scalar images based on image brightness do not accommodate pathologies. In the formation of the class posteriors, we can explicitly assign classes to the various healthy and pathological tissues. This allows us to potentially model the behaviors of the different tissues during the registration process.

Another potential application for this method is the registration of images acquired from scanners of different field-strength. Image set registration across different scanners becomes an increasingly important component in multi-center studies. For example, in studies of developmental changes covering multiple years, and in follow-up studies of diseases with change of scanner technology. Images acquired from different scanners potentially have different contrasts and different spatial distortions. Our new method may help to address these problems as the registration would be based on underlying anatomical structures rather than simply image intensities.

7 Conclusion

Image set registration is a generalization of pair-wise scale image registration where each image set is composed of an arbitrary number of scalar images. In this paper, we have presented a novel method for multi-modal image set registration and multi-class atlas formation. The method is modal-based and finds correspondences between underlying class structures using posterior mass functions. We use Kullback-Leibler divergence on the space of posteriors as the minimization of this distance maximizes Bayes probability of error and, hence, indistinguishability between two posteriors. This method extends to the problem of multi-class atlas formation via computing an intrinsic, and hence, unbiased, mean. The introduction of this unbiased mean makes this registration approach intrinsically inverse-consistent. We have presented results, for image set configurations of varying complexity, which suggest that this method produces image set registrations with low inverse-consistency error.

Acknowledgments

The authors would like to thank Matthieu Jomier for producing the class posterior mass functions used in the atlas formation and Dr. Mark Foskey for insightful discussions. This work was supported by NIBIB-NIH grant R01 EB000219, NIH-HLB grant R01 HL69808, DOD Prostate Cancer Research Program DAMD17-03-1-0134, NIMH grant MH064580 Longitudinal MRI Study of Brain Development in Fragile X, and the NDRC.

Contributor Information

Peter Lorenzen, Email: [email protected].

Marcel Prastawa, Email: [email protected].

Brad Davis, Email: [email protected].

Guido Gerig, Email: [email protected].

Elizabeth Bullitt, Email: [email protected].

Sarang Joshi, Email: [email protected].

References

1.Hermosillo G. PhD thesis. Universite de Nice - Sophia Antipolis; May, 2002. Variational methods for multimodal image matching. [Google Scholar]
2.D’Agostino E, Maes F, Vandermeulen D, Suetens P. An information theoretic approach for non-rigid image registration using voxel class probabilities. International Workshop on Biomedical Image Registration (WBIR), Vol. 2717 of Lecture Notes in Computer Science (LNCS); Springer-Verlag. 2003. pp. 122–131. [Google Scholar]
3.D’Agostino E, Maes F, Vandermeulen D, Suetens P. A viscous fluid model for multimodal non-rigid image registration using mutual information. Medical Image Analysis (MedIA) 2003;7(4):565–575. doi: 10.1016/s1361-8415(03)00039-2. [DOI] [PubMed] [Google Scholar]
4.Chan H-M, Chung ACS, Yu SCH, Norbash AWMW., III Multi-modal image registration by minimizing Kullback-Leibler distance between expected and observed joint class histograms. Proceedings of IEEE Computer Vision and Pattern Recognition (CVPR); 2003. pp. 570–576. IEEE. [Google Scholar]
5.Rueckert D, Hayes C, Studholme C, Summers P, Leach M, Hawkes DJ. Non-rigid registration of breast MR images using mutual information. Proceedings of Medical Image Computing and Computer-Assisted Intervention (MICCAI), Lecture Notes in Computer Science (LNCS); Springer-Verlag. 1998. pp. 1144–1152. [Google Scholar]
6.Miller MI, Joshi SC, Christensen G. Brain Warping. Ch. 7. Academic Press; San Diego: 1999. Large deformation fluid diffeomorphism for landmark and image matching; pp. 115–131. [Google Scholar]
7.Gaens T, Maes F, Vandermeulen D, Suetens P. Non-rigid multimodal image registration using mutual information. Proceedings of Medical Image Computing and Computer-Assisted Intervention (MICCAI), Lecture Notes in Computer Science (LNCS); Springer-Verlag. 1998. pp. 1099–1106. [Google Scholar]
8.Studholme C, Hill DLG, Hawkes DJ. An overlap invariant entropy measure of 3d medical image alignment. Pattern Recognition. 1999;32(1):71–86. [Google Scholar]
9.Lorenzen P, Joshi S. High-dimensional multi-modal image registration. International Workshop on Biomedical Image Registration (WBIR), Vol. 2717 of Lecture Notes in Computer Science (LNCS); Springer-Verlag. 2003. pp. 234–243. [Google Scholar]
10.Lorenzen P, Davis B, Joshi S. Model based symmetric information theorectic large deformation multi-modal image registsration. Proceedings of IEEE International Symposium on Biomedical Imaging (ISBI); 2004. pp. 720–723. [Google Scholar]
11.Davis B, Lorenzen P, Joshi S. Large deformation minimum mean squared error template estimation for computation anatomy. Proceedings of IEEE International Symposium on Biomedical Imaging (ISBI); 2004. pp. 173–176. [Google Scholar]
12.Lorenzen P, Davis B, Gerig G, Bullitt E, Joshi S. Multi-class posterior atlas formation via unbiased Kullback-Leibler template estimation. Proceedings of Medical Image Computing and Computer-Assisted Intervention (MICCAI), Lecture Notes in Computer Science (LNCS); Springer-Verlag. 2004. pp. 95–102. [Google Scholar]
13.Bhatia KK, Hajnal JV, Puri BK, Edwards AD, Ruekert D. Consistent groupwise non-rigid registration for atlas construction. Proceedings of IEEE International Symposium on Biomedical Imaging (ISBI); 2004. pp. 908–911. [Google Scholar]
14.Miller M, Banerjee A, Christensen G, Joshi S, Khaneja N, Grenander U, Matejic L. Statistical methods in computational anatomy. Statistical Methods in Medical Research. 1997;6:267–299. doi: 10.1177/096228029700600305. [DOI] [PubMed] [Google Scholar]
15.Grenander U, Miller M. Computational anatomy: an emerging discipline. Quarterly of Applied Mathematics. 1998;56:617–694. [Google Scholar]
16.Thompson P, Woods R, Mega M, Toga A. Mathmatical/computational challenges in creating deformable and probabilistic atlases of the human brain. Human Brain Mapping. 2000;9(2):81–92. doi: 10.1002/(SICI)1097-0193(200002)9:2<81::AID-HBM3>3.0.CO;2-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
17.Joshi S, Davis B, Jomier M, Gerig G. Unbiased diffeomorphic atlas construction for computational anatomy. To Appear in NeuroImage. doi: 10.1016/j.neuroimage.2004.07.068. [DOI] [PubMed] [Google Scholar]
18.Cachier P, Rey D. Symmetrization of the non-rigid registration problem using inversion-invariant energies: Application to multiple sclerosis. Proceedings of Medical Image Computing and Computer Assisted Intervention (MICCAI), Lecture Notes in Computer Science (LNCS); Springer-Verlag. 2002. pp. 472–481. [Google Scholar]
19.He J, Christensen GE. Large deformation inverse consistent elastic image registration. Information Processing in Medical Imaging (IPMI), Lecture Notes in Computer Science (LNCS); Springer-Verlag. 2003. pp. 438–449. [DOI] [PubMed] [Google Scholar]
20.Prastawa M, Moon N, Bullitt E, van Leemput K, Gerig G. Automatic brain tumor segmentation by subject specific modification of atlas priors. Academic Radiology. 2003;10:1341–1348. doi: 10.1016/s1076-6332(03)00506-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
21.van Leemput K, Maes F, Vandermeulen D, Suetens P. Automated model-based tissue classification of mr images of the brain. IEEE Transactions on Medical Imaging (TMI) 1999;18(10):897–908. doi: 10.1109/42.811270. [DOI] [PubMed] [Google Scholar]
22.Joshi S, Miller MI. Landmark matching via large deformation diffeomorphisms. IEEE Transactions on Image Processing. 2000;9(8):1357–1370. doi: 10.1109/83.855431. [DOI] [PubMed] [Google Scholar]
23.Kullback S, Leibler RA. On information and sufficiency. The Annals of Mathematical Statistics. 1951;22(1):79–86. [Google Scholar]
24.Cover T, Thomas J. Elements of Information Theory. John Wiley and Sons, Inc; New York: 1991. [Google Scholar]
25.Kailath T. The divergence and Bhattacharyya distance measures in signal selection. IEEE Transactions on Communication Theory. 1967;(1):52–60. [Google Scholar]
26.Jeffreys H. An invariant form for the prior probability in estimation problems. Proceedings of the Royal Society A. 1946;186:453–461. doi: 10.1098/rspa.1946.0056. [DOI] [PubMed] [Google Scholar]
27.Hoeffding W, Wolfowitz J. Distinguishability of sets of distributions. The Annals of Mathematical Statistics. 1958;29:700–718. [Google Scholar]
28.Toussaint GT. Comments on the divergence and Bhattacharyya distance measures in signal selection. IEEE Transactions on Communications. 1972;20(3):485–485. [Google Scholar]
29.Christensen GE, Rabbitt RD, Miller MI. Deformable templates using large deformation kinematics. IEEE Transactions on Image Processing (TIP) 1996;5(10):1435–1447. doi: 10.1109/83.536892. [DOI] [PubMed] [Google Scholar]
30.Joshi S, Lorenzen P, Gerig G, Bullitt E. Structural and radiometric asymmetry in brain images. Medical Image Analysis (MedIA) 2003;7(2):155–170. doi: 10.1016/s1361-8415(03)00002-1. [DOI] [PubMed] [Google Scholar]
31.Prastawa M, Bullitt E, Ho S, Gerig G. A brain tumor segmentation framework based on outlier dection. Medical Image Analysis (MedIA) 2004:275–283. doi: 10.1016/j.media.2004.06.007. [DOI] [PubMed] [Google Scholar]
32.van Leemput K, Maes F, Vandermeulen D, Suetens P. Automated model-based bias field correction of MR images of the brain. IEEE Transactions on Medical Imaging (TMI) 1999;18(10):885–896. doi: 10.1109/42.811268. [DOI] [PubMed] [Google Scholar]

[R1] 1.Hermosillo G. PhD thesis. Universite de Nice - Sophia Antipolis; May, 2002. Variational methods for multimodal image matching. [Google Scholar]

[R2] 2.D’Agostino E, Maes F, Vandermeulen D, Suetens P. An information theoretic approach for non-rigid image registration using voxel class probabilities. International Workshop on Biomedical Image Registration (WBIR), Vol. 2717 of Lecture Notes in Computer Science (LNCS); Springer-Verlag. 2003. pp. 122–131. [Google Scholar]

[R3] 3.D’Agostino E, Maes F, Vandermeulen D, Suetens P. A viscous fluid model for multimodal non-rigid image registration using mutual information. Medical Image Analysis (MedIA) 2003;7(4):565–575. doi: 10.1016/s1361-8415(03)00039-2. [DOI] [PubMed] [Google Scholar]

[R4] 4.Chan H-M, Chung ACS, Yu SCH, Norbash AWMW., III Multi-modal image registration by minimizing Kullback-Leibler distance between expected and observed joint class histograms. Proceedings of IEEE Computer Vision and Pattern Recognition (CVPR); 2003. pp. 570–576. IEEE. [Google Scholar]

[R5] 5.Rueckert D, Hayes C, Studholme C, Summers P, Leach M, Hawkes DJ. Non-rigid registration of breast MR images using mutual information. Proceedings of Medical Image Computing and Computer-Assisted Intervention (MICCAI), Lecture Notes in Computer Science (LNCS); Springer-Verlag. 1998. pp. 1144–1152. [Google Scholar]

[R6] 6.Miller MI, Joshi SC, Christensen G. Brain Warping. Ch. 7. Academic Press; San Diego: 1999. Large deformation fluid diffeomorphism for landmark and image matching; pp. 115–131. [Google Scholar]

[R7] 7.Gaens T, Maes F, Vandermeulen D, Suetens P. Non-rigid multimodal image registration using mutual information. Proceedings of Medical Image Computing and Computer-Assisted Intervention (MICCAI), Lecture Notes in Computer Science (LNCS); Springer-Verlag. 1998. pp. 1099–1106. [Google Scholar]

[R8] 8.Studholme C, Hill DLG, Hawkes DJ. An overlap invariant entropy measure of 3d medical image alignment. Pattern Recognition. 1999;32(1):71–86. [Google Scholar]

[R9] 9.Lorenzen P, Joshi S. High-dimensional multi-modal image registration. International Workshop on Biomedical Image Registration (WBIR), Vol. 2717 of Lecture Notes in Computer Science (LNCS); Springer-Verlag. 2003. pp. 234–243. [Google Scholar]

[R10] 10.Lorenzen P, Davis B, Joshi S. Model based symmetric information theorectic large deformation multi-modal image registsration. Proceedings of IEEE International Symposium on Biomedical Imaging (ISBI); 2004. pp. 720–723. [Google Scholar]

[R11] 11.Davis B, Lorenzen P, Joshi S. Large deformation minimum mean squared error template estimation for computation anatomy. Proceedings of IEEE International Symposium on Biomedical Imaging (ISBI); 2004. pp. 173–176. [Google Scholar]

[R12] 12.Lorenzen P, Davis B, Gerig G, Bullitt E, Joshi S. Multi-class posterior atlas formation via unbiased Kullback-Leibler template estimation. Proceedings of Medical Image Computing and Computer-Assisted Intervention (MICCAI), Lecture Notes in Computer Science (LNCS); Springer-Verlag. 2004. pp. 95–102. [Google Scholar]

[R13] 13.Bhatia KK, Hajnal JV, Puri BK, Edwards AD, Ruekert D. Consistent groupwise non-rigid registration for atlas construction. Proceedings of IEEE International Symposium on Biomedical Imaging (ISBI); 2004. pp. 908–911. [Google Scholar]

[R14] 14.Miller M, Banerjee A, Christensen G, Joshi S, Khaneja N, Grenander U, Matejic L. Statistical methods in computational anatomy. Statistical Methods in Medical Research. 1997;6:267–299. doi: 10.1177/096228029700600305. [DOI] [PubMed] [Google Scholar]

[R15] 15.Grenander U, Miller M. Computational anatomy: an emerging discipline. Quarterly of Applied Mathematics. 1998;56:617–694. [Google Scholar]

[R16] 16.Thompson P, Woods R, Mega M, Toga A. Mathmatical/computational challenges in creating deformable and probabilistic atlases of the human brain. Human Brain Mapping. 2000;9(2):81–92. doi: 10.1002/(SICI)1097-0193(200002)9:2<81::AID-HBM3>3.0.CO;2-8. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R17] 17.Joshi S, Davis B, Jomier M, Gerig G. Unbiased diffeomorphic atlas construction for computational anatomy. To Appear in NeuroImage. doi: 10.1016/j.neuroimage.2004.07.068. [DOI] [PubMed] [Google Scholar]

[R18] 18.Cachier P, Rey D. Symmetrization of the non-rigid registration problem using inversion-invariant energies: Application to multiple sclerosis. Proceedings of Medical Image Computing and Computer Assisted Intervention (MICCAI), Lecture Notes in Computer Science (LNCS); Springer-Verlag. 2002. pp. 472–481. [Google Scholar]

[R19] 19.He J, Christensen GE. Large deformation inverse consistent elastic image registration. Information Processing in Medical Imaging (IPMI), Lecture Notes in Computer Science (LNCS); Springer-Verlag. 2003. pp. 438–449. [DOI] [PubMed] [Google Scholar]

[R20] 20.Prastawa M, Moon N, Bullitt E, van Leemput K, Gerig G. Automatic brain tumor segmentation by subject specific modification of atlas priors. Academic Radiology. 2003;10:1341–1348. doi: 10.1016/s1076-6332(03)00506-3. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R21] 21.van Leemput K, Maes F, Vandermeulen D, Suetens P. Automated model-based tissue classification of mr images of the brain. IEEE Transactions on Medical Imaging (TMI) 1999;18(10):897–908. doi: 10.1109/42.811270. [DOI] [PubMed] [Google Scholar]

[R22] 22.Joshi S, Miller MI. Landmark matching via large deformation diffeomorphisms. IEEE Transactions on Image Processing. 2000;9(8):1357–1370. doi: 10.1109/83.855431. [DOI] [PubMed] [Google Scholar]

[R23] 23.Kullback S, Leibler RA. On information and sufficiency. The Annals of Mathematical Statistics. 1951;22(1):79–86. [Google Scholar]

[R24] 24.Cover T, Thomas J. Elements of Information Theory. John Wiley and Sons, Inc; New York: 1991. [Google Scholar]

[R25] 25.Kailath T. The divergence and Bhattacharyya distance measures in signal selection. IEEE Transactions on Communication Theory. 1967;(1):52–60. [Google Scholar]

[R26] 26.Jeffreys H. An invariant form for the prior probability in estimation problems. Proceedings of the Royal Society A. 1946;186:453–461. doi: 10.1098/rspa.1946.0056. [DOI] [PubMed] [Google Scholar]

[R27] 27.Hoeffding W, Wolfowitz J. Distinguishability of sets of distributions. The Annals of Mathematical Statistics. 1958;29:700–718. [Google Scholar]

[R28] 28.Toussaint GT. Comments on the divergence and Bhattacharyya distance measures in signal selection. IEEE Transactions on Communications. 1972;20(3):485–485. [Google Scholar]

[R29] 29.Christensen GE, Rabbitt RD, Miller MI. Deformable templates using large deformation kinematics. IEEE Transactions on Image Processing (TIP) 1996;5(10):1435–1447. doi: 10.1109/83.536892. [DOI] [PubMed] [Google Scholar]

[R30] 30.Joshi S, Lorenzen P, Gerig G, Bullitt E. Structural and radiometric asymmetry in brain images. Medical Image Analysis (MedIA) 2003;7(2):155–170. doi: 10.1016/s1361-8415(03)00002-1. [DOI] [PubMed] [Google Scholar]

[R31] 31.Prastawa M, Bullitt E, Ho S, Gerig G. A brain tumor segmentation framework based on outlier dection. Medical Image Analysis (MedIA) 2004:275–283. doi: 10.1016/j.media.2004.06.007. [DOI] [PubMed] [Google Scholar]

[R32] 32.van Leemput K, Maes F, Vandermeulen D, Suetens P. Automated model-based bias field correction of MR images of the brain. IEEE Transactions on Medical Imaging (TMI) 1999;18(10):885–896. doi: 10.1109/42.811268. [DOI] [PubMed] [Google Scholar]

PERMALINK

Multi-Modal Image Set Registration and Atlas Formation

Peter Lorenzen

Marcel Prastawa

Brad Davis

Guido Gerig

Elizabeth Bullitt

Sarang Joshi

Abstract

1 Introduction

1.1 Model-Based Multi-Modal Image Set Registration

1.2 Multi-Class Atlas Formation

1.3 Inverse Consistent Registration

2 Methodology: Atlas Formation

2.1 Bayesian Framework

2.2 Large Deformation Multi-Class Atlas Formation

Figure 1. Atlas Formation.

Figure 2. Velocity Fields.

2.3 Kullback-Leibler Divergence

Definition 1

2.3.1 Bayes Probability of Error

Figure 3. Bayes Probability of Error for Two Distributions.

2.3.2 Bounds on P(error) for Our Two-Hypothesis Problem

2.4 Registration

2.5 Implementation

3 Methodology: Image Set Registration

Figure 4. Registration Framework.

3.1 Bayesian Framework

3.2 Registration

3.3 Implementation

4 Results: Atlas Formation

Figure 5. Population of Class Posteriors.

Figure 6. Atlas Construction.

5 Results: Image Set Registration

5.1 Data Preprocessing

Figure 7. Subject One.

Figure 8. Subject Two.

5.2 Registration Experiments

5.2.2 Bi-Modal/Bi-Modal (mutually exclusive) Registration

Figure 9. Forward Mapping.

Figure 10. Backward Mapping.

5.2.3 Inverse-Consistency

6 Discussion

7 Conclusion

Acknowledgments

Contributor Information

References

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases