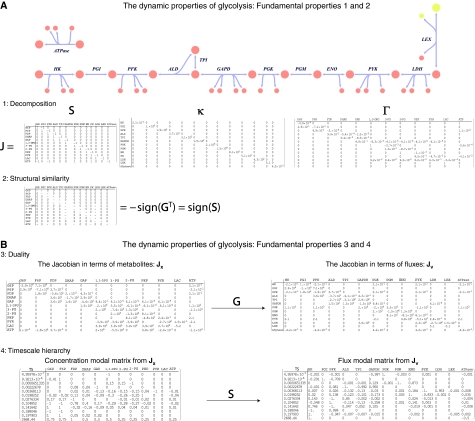
Figure 3.
(A) An example of the first two properties for the glycolytic pathway. A reaction map of the glycolytic pathway is shown. The decomposition of the Jacobian (Jx) into the stoichiometric, κ, and Γ matrices follows below (1−norm used for the factorization of Γ). The negative transpose of the gradient matrix is shown directly below the stoichiometric matrix, demonstrating the structural similarity. (B) Explicit illustration of the third and fourth properties via the resulting data matrices. The Jacobian duals are shown; they are related by the gradient matrix. Hierarchical analysis can be carried out of the network in terms of metabolites or fluxes. The resultant modal matrices can be related to one another via the stoichiometric matrix. As illustrated in Figure 4, sometimes it is convenient to think about the hierarchical structure in terms of metabolites and sometimes it is more intuitive to think in terms of the fluxes. The network was constructed using equilibrium constants and concentrations from a kinetic red cell model, which has been validated in the literature. Network dynamics were then described using mass action kinetics for a particular steady state. Abbreviations: ALD, fructose-bisphosphate aldolase; ATPase, ATP hydrolysis (demand/utilization); ENO, enolase; GAPD, glyceraldehyde phosphate dehydrogenase; HK, hexokinase; LDH, lactate dehydrogenase; LEX, lactate transporter; PFK, phosphofructokinase; PGI, phosphoglucoisomerase; PGK, phosphoglucokinase; PGM, phosphoglucomutase; PYK, pyruvate kinase; TPI, triose-phosphate isomerase; TS, timescales in hours.