Abstract
Candidate single-nucleotide polymorphisms (SNPs) were analyzed for associations to an unselected whole genome pool of tumor mRNA transcripts in 50 unrelated patients with breast cancer. SNPs were selected from 203 candidate genes of the reactive oxygen species pathway. We describe a general statistical framework for the simultaneous analysis of gene expression data and SNP genotype data measured for the same cohort, which revealed significant associations between subsets of SNPs and transcripts, shedding light on the underlying biology. We identified SNPs in EGF, IL1A, MAPK8, XPC, SOD2, and ALOX12 that are associated with the expression patterns of a significant number of transcripts, indicating the presence of regulatory SNPs in these genes. SNPs were found to act in trans in a total of 115 genes. SNPs in 43 of these 115 genes were found to act both in cis and in trans. Finally, subsets of SNPs that share significantly many common associations with a set of transcripts (biclusters) were identified. The subsets of transcripts that are significantly associated with the same set of SNPs or to a single SNP were shown to be functionally coherent in Gene Ontology and pathway analyses and coexpressed in other independent data sets, suggesting that many of the observed associations are within the same functional pathways. To our knowledge, this article is the first study to correlate SNP genotype data in the germ line with somatic gene expression data in breast tumors. It provides the statistical framework for further genotype expression correlation studies in cancer data sets.
Keywords: genotype–phenotype interaction, locus control region, single-nucleotide polymorphism expression association
Recent work (1–5) has demonstrated the effects of genetic variation on mRNA expression. Given the increasing clinical importance of microarray expression for classification of breast tumors and the different biology it may reveal, the elucidation of its genetic background is of considerable importance. In a recent report Morley et al. (1) described a broad study of the genetic determinants of normal expression variation in humans. The authors used microarrays to measure the baseline expression levels of ≈8,500 genes, or transcripts, in immortalized B cells from members of Centre d’Etude du Polymorphisme Humain Utah pedigrees. They selected 3,554 genes that varied more between individuals than between replicates and used these as quantitative traits to be mapped into genomic locations. They used public genotype information to carry out linkage analysis for these expression phenotypes in 14 Centre d’Etude du Polymorphisme Humain families. They found high linkage signals for 984 of the transcripts [at P < 0.05, leading to a false discovery rate (FDR) of ≈0.2]. Interestingly, they identified regions that show linkage signals to many of the transcripts, and they proposed that these regions can point toward master regulators of baseline expression levels both in cis and in trans. Regulation hotspots were notably identified on 14q32 and 20q13.
Choosing family members with Mendelian inheritance of both single-nucleotide polymorphisms (SNPs) and mRNA expression facilitated the data analysis in Morley et al. (1). In the current work, we report observations from a study with a different design, performing actual genotyping of 203 genes in 50 unrelated breast cancer patients whose tumors have previously been analyzed by genome-wide expression by using microarrays. Our main goal of this study was to explore the genetic determinants of expression in breast tumors. The candidate genes selected for genotyping were from predefined pathways. The antineoplastic effect of both chemotherapy and radiation therapy is exerted either by directly attacking cellular macromolecules, including DNA, or by generating reactive oxygen species (ROS) and their by-products. Hence, the genes selected to create the genotype profile of patients treated with radiation therapy and chemotherapy are all involved in regulating the redox level in the cells, in signaling, or in DNA damage repair caused by ROS. We computed the association between each genotype locus and each measured transcript and searched the resulting associated data for statistically significant structures. Despite the notion that expression differences caused by genetic instability, rearrangements, and altered methylation occur in tumors during progression of the disease, significant associations were observed above random expectation, pointing to putative regulatory SNPs.
Results and Discussion
In this study, we included 50 Norwegian patients with locally advanced breast cancer where mRNA expression data on their tumor as well as a blood sample for genotyping were available. Description of the patients and references to the previously published expression data are in Table 4, which is published as supporting information on the PNAS web site. Microarray expression data were previously analyzed and were shown to lead to a robust tumor classification with strong prognostic impact (6–8).
SNP Mining and Genotype Results.
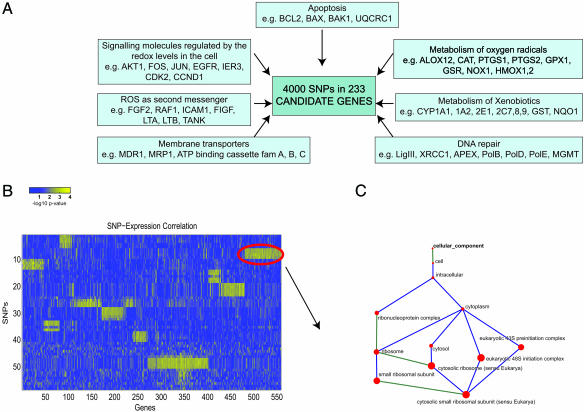
The candidate genes for SNP analysis were selected from ≈4,000 MEDLINE entries and different databases (Online Mendelian Inheritance in Man and Human Genome Organization) to create the genotype profile of all genes involved in the regulation of the redox level in the cells, ROS-mediated signaling, and repair of DNA damage caused by ROS (Fig. 1). A total of 1,030 SNPs was selected by the SNP data mining approach described in Edvardsen et al. (9). Briefly, each of the candidate genes extracted from PubMed recourses was matched with the official Human Genome Organization gene name, and information about sequence variation was obtained. The annotation of each SNP was followed in several databases, and data on its frequency in the Caucasian population were obtained. Approximately 4,000 SNPs could be identified in the initial 233 candidate genes by computer annotation (Fig. 1A). SNP selection was performed based on putative gene function and SNP frequencies. We performed actual genotyping of 1,030 of these SNPs in 213 genes on chromosomes 1–X. Of these, 725 (≈69%) were successfully genotyped in the first round. One hundred four (≈14.3%) of the 725 genotyped SNPs were with frequency of <5%. An additional 38 SNPs were not in Hardy–Weinberg equilibrium (≈5%), leaving 583 SNPs for association studies. We studied the tumor genome-wide expression effect of these 583 SNPs that reside in 203 of the selected genes (1–19 SNPs per gene).
Fig. 1.
Data mining and analysis workflow. (A) A total of 583 SNPs in 203 candidate genes from the ROS metabolizing and signaling pathway were selected from an initial pool of 4,000 SNPs in 233 genes. These 583 selected SNPs were analyzed for associations to 3,351 mRNA transcripts from a whole-genome expression analysis, filtered for signal quality (ratio of spot intensity over background exceeding 1.5 in at least 80% of the experiments in each dye channel). A subset of SNPs and a subset of transcripts that belong to biclusters were identified. (B) A heat map of −log10 (P value) of SNP–transcript associations, with range from 0 to −log10(9.5E-005) = 4.02. Bright yellow indicates significant associations. Rows and columns are reordered to highlight biclusters, subsets of SNPs, and transcripts that share significantly many common significant associations (one example is highlighted with a red oval). (C) GO analysis was used to study the overrepresentation of GO functional classes in these sets of mRNA transcripts. The size of the corresponding node of the GO tree is proportional to the significance of the overrepresentation of the term. [B and C are reproduced with permission from ref. 21 (Copyright 2005, IEEE).]
Statistical Analysis of SNP–mRNA Expression Associations.
Three complementary analyses [ANOVA, quantitative mutual information score (QMIS), and leave-one-out cross-validation (LOOCV)] (10–12) were used to analyze the data and to demonstrate possible parametric and nonparametric approaches to assess SNP–transcript association. We computed an association matrix whose entries represent the P values of association for every SNP/transcript pair (11). Let N and M denote the number of SNPs and transcripts, respectively. For each pair (s, t) of SNP and transcript, we computed an association score and a corresponding P value, Pst, using one of the three methods described (see Materials and Methods). The resulting N-by-M matrix P is called the association matrix. Given a significance threshold 0 < P < 1, we state that s is associated with t if Pst < P. SNPs whose corresponding rows have significantly many entries with low P values are potential regulators of expression levels. Subsets of SNPs and subsets of transcripts that belong to biclusters were identified by a method adapted from Tanay et al. (13) (Fig. 1B).
Significant Associations.
SNP expression associations with the best P values (P < 0.001) detected by both ANOVA and QMIS revealed regulatory SNPs in trans in 115 genes, such as AKT1, AKT2, CALM3, CDC25B, DPYD, FOS, IER3, IGF1R, IGF2, IGF2R, IL8, IL10, IL10RA, NFKB1, PRKCA, PPP3CA, PPP2R4, GCLM, TGFBR3, PPP1R2, and others (see the full list in Table 5, which is published as supporting information on the PNAS web site, including P values for all SNP–transcript pairs, where 10−6 was the lowest). For example, the presence of the variant G or C allele for SNPs in PPP1R2 and TGFBR3, respectively, led to an increased expression of QDPR and FANCA, even more pronounced in the homozygous variant genotype (Fig. 4, which is published as supporting information on the PNAS web site). Of the 115 genes, 43 genes harbored SNPs associated with mRNA expression both in cis, i.e., to the expression of their own gene, and in trans by both QMIS and ANOVA when requiring P < 0.001 in both methods (highlighted in Table 1; P values for each association are in Tables 5 and 6, which are published as supporting information on the PNAS web site). For example, SNPs that significantly associated with the expression of their own genes were found in GSTM3, XPC (two SNPs), GSTA4, GSTP1, ABCC1 (two SNPs), TYMS (four SNPs), CALM3, and MAPK1 (see the full list in Table 6). When we broadened the search for in cis interactions with mRNA coded 4 Mbp upstream and downstream of an SNP, 107 significant associations were found at P < 0.025 (Table 6; some exemplified in Fig. 5, which is published as supporting information on the PNAS web site). Some of the SNPs regulating in cis form are in strong linkage disequilibrium (LD).
Table 1.
Genes where SND-expression associations were observed in both cis and trans
| Gene | Cytoband | Gene | Cytoband |
|---|---|---|---|
| GSTM3 | 1p13.3 | PPP2R4 | 9q34 |
| DPYD | 1p22 | BCCIP | 10q26.1 |
| GCLM | 1p22.1 | PPP1R1A | 12q13.13 |
| IL10 | 1q31-q32 | LIG4 | 13q33-q34 |
| EPHX1 | 1q42.1 | NFKBIA | 14q13 |
| XDH | 2p23-p22 | TGFB3 | 14q24 |
| RAF1, XPC | 3p25 | GPX2 | 14q24.1 |
| PPP1R2 | 3q29 | ABCC1 | 16p13.1 |
| SOD3 | 4p16.3-q21 | HMOX2 | 16p13.3 |
| UGT2A1 | 4q13 | NQO1 | 16q22.1 |
| IL8 | 4q13-q21 | COX10 | 17p12-17p11.2 |
| PPP3CA | 4q21-q24 | ALOX12 | 17p13.1 |
| GSTA4 | 6p12.1 | PIN1 | 19p13 |
| BAK1, IER3 | 6p21.3 | ICAM5, XRCC1 | 19p13.2 |
| NOX3 | 6q25.1-q26 | CALM3 | 19q13.2-q13.3 |
| SOD2 | 6q25.3 | POLD1 | 19q13.3 |
| IGF2R | 6q26 | PCNA | 20pter-p12 |
| PPP1R9A | 7q21.3 | IL10RB | 21q22.1-q22.2 |
| EPHX2 | 8p21-p12 | TXNRD2 | 22q11.21 |
| PDGFRL | 8p22-p21.3 | PRKCABP | 22q13.1 |
For SNP–transcript pairs with strong associations supported on many samples we expected both QMIS and ANOVA P values to be small but not necessarily in the same range. For SNPs with small number of samples with a given genotype, we can see disagreement between the scores. ANOVA and QMIS P values were calculated based on different assumptions about the distributions of genotypes and expression values for each SNP association pair; these assumptions may not necessarily hold for a small number of samples. Therefore, restricting our analysis to SNP–transcript pairs significant with respect to both scores is an additional way to eliminate false positives. Table 2 shows the number of SNP–transcript pairs for various P value cutoffs and sizes of corresponding overlaps. The last column shows the expected overlap between randomly selected subsets of corresponding sizes. Note that the actual overlap in SNP–transcript pairs is much larger than was expected in a random case.
Table 2.
Number of SNP–transcript pairs for various P value cutoffs and sizes of corresponding overlap
| P value | No. of pairs |
Overlap of ANOVA and QMIS |
||
|---|---|---|---|---|
| ANOVA | QMIS | Observed | Expected | |
| 1.00 × 10−6 | 41 | 7 | 0 | 0.0 |
| 1.00 × 10−5 | 121 | 79 | 13 | 0.0 |
| 0.0001 | 506 | 769 | 182 | 0.2 |
| 0.001 | 2,691 | 8,667 | 2,827 | 12.0 |
| 0.01 | 19,771 | 97,028 | 47,408 | 990.4 |
| 0.1 | 181,708 | 1,015,752 | 786,482 | 95,292.7 |
| 1 | 1,936,878 | 1,930,520 | 1,936,878 | 1,936,878 |
LOOCV analysis revealed cases in which the expression of only one transcript was sufficient to correctly classify the cases according to their genotypes. For example, the expression of TFF1 [trefoil factor 1 (breast cancer, estrogen-inducible sequence)] on 21q22.3 was sufficient to correctly predict all of the genotypes for an SNP (rs 2228001) in the XPC gene on 3p25, with a success rate of 0.9, and addition of other genes did not improve the classification. Similarly, the expression of YARS2 on 12p11.21 was sufficient to predict alone the grouping according to the genotype in rs881878 of EGF on 4q25 (Table 7, which is published as supporting information on the PNAS web site).
We identified SNPs in EGF, IL1A, MAPK8, XPC, SOD2, and ALOX12 genes whose associations to gene expression are significant under all three methods, namely ANOVA and QMIS with P <0.001 and classification success of LOOCV analysis >90%, indicating the presence of regulatory SNPs in these genes.
Statistical Overabundance of Significant Associations.
We applied FDR analysis (14) to compare the actual association matrix to random data. FDR measures the ratio of expected and observed numbers of SNP–transcript association pairs with a given score or better. The number of associations in the data were determined by counting the number of entries in the association matrix less than or equal to a given threshold. For QMIS, 769 SNP–transcript association pairs with P ≤ 1.0E-04 were observed. In random data one may expect to find only 150 such pairs, as inferred from QMIS P value and the size of the association matrix, which represents an FDR of 0.2 (Fig. 2). Note that one SNP can show significant association to more than one transcript. The graphical presentation of the distributions of observed and expected numbers of SNP–transcript pairs with a certain P value or lower for QMIS is shown in Fig. 2. Right shows the corresponding FDR. For the ANOVA scores (Fig. 2 Left), 571 SNP–transcript association pairs with P ≤ 1.0E-04 were observed, yielding a FDR of 0.6 as estimated from permuted data (Fig. 6A, which is published as supporting information on the PNAS web site) (15). The level of significance (P < 1.0E-04) may not seem to be stringent enough for this type of study with a huge burden of multiple tests. To address this issue and to assess the true significance of the results, we performed an overabundance analysis and estimated the distribution of ANOVA P values using simulations. To assess the baseline false-positive rate, 50 random SNPs in different genes were selected, and genotype data were permuted 100 times. For P ≤ 1.0E-05, FDR = 0.55, and for P ≤ 1.0E-04, FDR = 0.7. The observed and expected ANOVA P values are shown in Fig. 6B, and it can be seen that they are very similar to the results shown in Fig. 6A.
Fig. 2.
Overabundance analysis for QMIS-based associations. Left shows a comparison of distributions of observed and expected numbers of SNP–transcript pairs with a certain P value or lower. [Reproduced with permission from ref. 21 (Copyright 2005, IEEE).] Inset shows the same restricted to P values between 1.0E-06 and 1.0E-04. Right shows the corresponding FDR. P values were computed exactly under a null model of uniform distribution of SNP genotype patterns of the same mixture.
Master Regulators.
SNP loci with an exceptionally large set of significantly associated transcripts are putative regulators of many transcripts. They potentially affect the expression levels or the mode of operation of transcription factors or of noncoding RNA-mediated regulation, directly or indirectly. Thus, these SNPs affect the transcription or degradation rates and hence the expression levels of many transcripts. SNPs that had exceptionally dense rows in the association matrix, P, belong to the genes PRKCA, CALM3, CYP2C19, IGF1R, IGF2R, and XDH. An exact definition of row density is given in ref. 15. For some of the putative master-regulating genes (IGF2R and CALM3) associations both in cis and in trans were detected (Table 1).
Functional Grouping of Regulated Transcript, Pathway, and Gene Ontology (GO) Analysis.
The trans interactions observed here suggest both “positional” and “functional” explanations. The positional scenario may involve either LD or epigenetic events such as common domains of relaxed chromatin structure along the chromosomes (16). The functional scenario may involve interactions of the kind between receptors and their ligands, transcription factors, and genes under their control, the genes for which do not have to reside in vicinity to each other. Of that kind, we observed a strong association between SNPs in several growth factors and the expression of their receptors like EGF/EGFR, IL1/IL1R, and TGFB2/TGFBR1–3. In fact, in this study we used the genotypes from a given predefined pathway (the ROS metabolizing and signaling pathway) enriched for GO terms like ATP binding, phosphate metabolism, phosphorylation, and tyrosine kinase activity to search for associations from an unselected pool of whole-genome mRNA transcripts. If we inversely examine the GO terms of the mRNA that we find associated with these SNPs (Table 8, which is published as supporting information on the PNAS web site), we often find the same GO terms as for the candidate genes (Fig. 7, which is published as supporting information on the PNAS web site), suggesting that the observed associations are within the same functional pathway.
A Common Set of SNPs Associated with a Common Set of Transcripts (Biclusters).
A bicluster is a submatrix of the association matrix, that is, a subset of SNPs and transcripts. The goal of the bicluster analysis is to identify significantly dense biclusters, in which the participating SNPs share significantly many common associations with the participating transcripts (Fig. 1B, yellow rectangles). When several SNP loci, especially when not in LD, associate with the same transcript or group of transcripts, this may be evidence of this expression phenotype being a complex trait, affected by several genetic events. Several significant biclusters were found in the data, one of them consisting of four SNPs (in IL1B, IER3, and NOX3, all related to stress response) and 82 transcripts (see the full list in Table 8). The GO term “cytosolic small ribosomal subunit” was significantly overrepresented in this set of transcripts (Bonferroni corrected P = 0.002) together with other related GO terms (Fig. 1C). When the same set of loci commonly associate with a large number of transcripts, we have cross-confirmation of the individual associations as well as a possible multilocus effect on a pathway or a biological process.
Common Blocks of Regulatory SNPs.
We identified associations of SNPs spanning over several genes like the transcription factors NFKB1, EGF, and FGF2 spanning 20.3 Mb of 4q24–26 as well as a cluster of genes on 11q13: CCND1, CCS, and GSTP1 associated with a large number of transcripts. These clusters of SNPs were found to be in strong LD (data not shown). When multiple SNPs in the same gene were studied for associations to groups of transcripts, the latter were found often to share a common pathway (Table 9, which is published as supporting information on the PNAS web site). In agreement with Morley et al. (1), who reported 14q32 as a master regulator locus, we found 12 SNPs in that locus containing cancer-related genes like AKT1, MAPK3, CDC42BPB, TNFAIP2, and TRAF3 associated with the expression of 38 genes at P < 0.01.
Genomic Clusters of Associated Transcripts.
Some of the transcripts associated with the same SNP or set of SNPs tended to cluster to common chromosomal regions, as observed in the Centre d’Etude du Polymorphisme Humain families (1). For instance, IL8-associated transcripts KPNA2, FALZ, HN1, and SLC9A3 reside on 17q23-q25; MAPK8-associated transcripts RARRES and SIAT4C reside on 11q23-q23.3, etc. If we plot the P values as a measure of the association between different SNPs and the associated transcripts across all chromosomes we observe a nonrandom distribution, as exemplified in Fig. 8, which is published as supporting information on the PNAS web site, for a stretch of 25 Mb on 17p21. This observation suggests that even in trans interactions are not at random but with transcripts that tend to cluster together on other chromosomes.
Coherent Expression Patterns.
We also studied the pairwise correlations of the expression levels of transcripts associated with the same SNP at P < 0.01 or a set of SNPs for the same gene (Fig. 3). For many such sets of transcripts, the average pairwise correlation values were significantly higher than the random expectation. Correlations were computed as described in Materials and Methods, and the observed values were compared to a distribution obtained by randomly drawing 100 transcript sets of the same size. The observed correlation z scores for associated sets of transcripts, together with properties of the null distributions, are shown in Fig. 3A and Table 3. Furthermore, we performed the same analysis using an independent breast cancer expression data set (Fig. 3B) (17). For several sets of transcripts, the z scores of transcript-to-transcript correlation, as computed from the independent data, were highly significant (Fig. 3 and Table 3), strongly validating the observed associations in our data set. Sets with high z scores in both data sets include the set of transcripts associated with SNPs in ABCB1, BAK, AKT2, and ABCC1 genes. ABCB1 (MDR1) is strongly related to drug resistance in cancer as well as in other conditions. The set of transcripts associated with genetic variants of ABCB1 (Table 10, which is published as supporting information on the PNAS web site) as observed in this study and validated by coherent expression patterns in van’t Veer et al.’s data (17), included an overrepresentation (P < 3E-07) of genes from the Kyoto Encyclopedia of Genes and Genomes human proteasome pathway such as PSMA1, PSMA5, and PSMC6, which might hold the key to better understanding the mechanisms of drug resistance.
Fig. 3.
Pairwise expression correlation of transcripts associated with the same SNP gene in two data sets. (A) Observed and expected correlation z scores for transcript subsets associated with SNPs in each candidate SNP gene. Expected distribution of z scores is computed as the correlation of n randomly selected transcripts for each of transcript set of size n. For each n, 100 random subsets were drawn. Error bars correspond to 1 SD. (B) z scores for the expression correlation of the corresponding subsets of transcripts in another breast cancer data set (17). Sets of transcripts associated with SNPs in ABCB1, BAK1, AKT2, and ABCC1 genes have expression correlation z scores in both data sets. Note that transcript sets are not ordered in the same way in both plots.
Table 3.
Pairwise correlations of the expression levels of n transcripts (number given in “Size”) associated with an SNP or set of SNPs in a gene (P < 0.01)
| Genes | Size | z score | Size, van’t Veer et al.’s data (17) | z score, van’t Veer et al.’s data (17) |
|---|---|---|---|---|
| Transcripts associated with CALM3 | 169 | 27.04 | 119 | 2.439 |
| Transcripts associated with CDC42BPB | 52 | 25.66 | 15 | −1.084 |
| Transcripts associated with GPX4 | 81 | 19.05 | 15 | −0.002 |
| Transcripts associated with COX10 | 65 | 18.93 | 5 | −0.580 |
| Transcripts associated with ABCB1 | 77 | 18.76 | 54 | 14.215 |
| Transcripts associated with BAK1 | 43 | 15.53 | 31 | 13.376 |
| Transcripts associated with GSTM3 | 39 | 13.91 | 3 | 0.250 |
| Transcripts associated with MAPK9 | 37 | 12.94 | 8 | 0.032 |
| Transcripts associated with AKT2 | 47 | 12.82 | 26 | 4.119 |
| Transcripts associated with TXNRD2 | 36 | 12.77 | 35 | 1.652 |
| Transcripts associated with II10RA | 40 | 12.30 | 24 | 0.095 |
| Transcripts associated with IL10RB | 26 | 12.18 | 6 | −1.532 |
| Transcripts associated with PPP1R15A | 50 | 10.13 | 6 | −1.473 |
| Transcripts associated with ABCC1 | 75 | 10.07 | 55 | 5.465 |
Conclusion
To our knowledge, this is the first study to correlate SNP genotype data in the germ line with somatic gene expression data in breast tumors. This article provides the statistical framework for further genotype expression correlation studies to cancer data sets. In summary, three different statistical approaches (QMIS, ANOVA, and LOOCV) were used to assess genetic association between SNPs in genes from ROS pathways to mRNA expression levels. For SNPs in EGF, IL1A, MAPK8, XPC, SOD2, and ALOX12, we found the strongest evidence of association according to all three methods. In addition, SNPs significantly associated with exceptionally large sets of transcripts were identified by QMIS and ANOVA in genes such as PRKCA, CALM3, CYP2C19, IGF1R, IGF2R, and XDH. To further understand and validate the existence of such large sets of transcripts associated with SNPs in trans, we (i) identified groups of SNPs that together are associated with a common set of transcripts (biclusters), (ii) searched for significant overrepresentation of pathway and GO terms suggesting common biological function of these associated transcripts, and (iii) provided evidence for a coherent expression of the associated transcripts in the present data set and in an independent expression data set (17). In total, 769 SNP–transcript association pairs with P ≤ 1.0E-04 were observed, compared with only 150 expected in a random data set.
SNP signals associated with gene expression were observed in lymphoblastoid cell lines from healthy individuals (1, 5), and in the present study, SNPs in blood DNA from breast cancer patients were associated with expression in the tumor tissue. We may expect different, stronger signals in our study, admitting the existence of strong SNPs or expression susceptibility pattern associated with breast cancer per se. Factors that may influence mRNA expression in a tumor-like somatic mutations, genomic instability, different steady states of expression as a result of external insult (drug), and tissue and cell specificity may obscure the SNP association. Such factors may partly be the reason for the relatively high FDR. A comparable FDR level to that reported in the study of Morley et al. (1) was observed for the QMIS analysis (0.2). In our study, we describe additional analyses, including bicluster analysis, functional enrichment, and the expression coherence analysis. We also study more complex structures in the association matrix. These yield more statistically significant findings, as reported. The high FDR across the whole range of P values did not allow us to define the P value cutoff for further analysis, and we used a nominal cutoff of 0.001 for presenting potentially interesting association pairs in Table 5 and a cutoff of 0.01 for bicluster and functional enrichment analysis. Indeed, we recognized important regulators of whole pathways such as NFKB1, EGF, and FGF2 among the genes in which SNPs have impact on mRNA expression of several genes. Some of the associations we report here are further validated by analyzing an independent breast cancer data set. Still more profound functional studies are necessary to prove the causal relationship and to grant these SNPs “regulators” status.
Materials and Methods
Genotype and Haplotype Analyses.
Genotyping was performed as described in Edvardsen et al. (9). LD estimation for the SNPs shown to be associated with transcripts in cis and exemplified in Fig. 5 was performed by using haploview. haploview estimates the maximum-likelihood values of the four gamete frequencies, from which the D′, logarithm of odds, and r2 calculations are derived (18). Conformance with Hardy–Weinberg equilibrium is computed by using the Fisher exact test.
Statistical and Bioinformatics Analyses.
ANOVA.
For each SNP locus and each transcript, we computed the one-way ANOVA P value for the expression vector and grouping of the samples based on SNP locus genotypes (10). The null hypothesis here is that expression level distributions are the same, regardless of the genotype class.
QMIS.
For an SNP locus s and an expression vector q of transcript t, let G be a partition of samples induced by the genotype values at locus s. For an expression level threshold p, let Cp be a partition of samples defined by the q < p and q ≥ p. The mutual information score (MIS) is the difference between the entropy of the partition Cp and the conditional entropy of Cp given G: MIS(Cp, G) = H(Cp) − H(Cp|G), where H is the entropy function. Define the QMIS to be the maximum possible MIS, i.e., QMIS(C, G) = maxmin(q)≤p≤max(q)MIS(Cp, G). An exact P value for the mutual information score can be computed exactly by an efficient exhaustive approach (11). The null hypothesis here is that genotype values have the same distribution, regardless of expression levels. A total of 578 × 3,351 = 1,936,878 association tests were performed for each ANOVA and QMIS analysis.
LOOCV.
LOOCV was used to further confirm strong associations. For a given SNP in the data set, we used its genotypes to group samples. For each grouping we ran LOOCV analysis, trying to predict from the expression data which genotype group each sample belongs to (similar to the methods described in ref. 12). Thus, we performed 583 LOOCV runs and selected cases that had classification success >90%, further restricted to SNPs with at least six cases in each of the three genotype groups.
Properties of the Association Matrix.
We studied the association matrix P, searching for the following structures:
Overall overabundance of associated pairs: we assessed the overall significance of the observed association between genotypes and expression phenotypes by comparing it to a null model.
Potential master regulators: we seek rows and columns in P that have significantly many entries with strong P values. Such structures represent the effect of this locus on many transcripts and suggest the presence of a regulation element. When several SNPs reside in the same gene, these are combined for this analysis. We further study the transcripts that are potentially regulated by a gene or associated with an SNP locus using expression correlation and external information as described below.
Biclusters: a bicluster is a submatrix of P. We adapt the methods of Tanay et al. (13) to find significantly dense biclusters, in which the participating SNPs share significantly many common associations with the participating transcripts (see Fig. 1B). When several SNP loci, especially when not in LD, associate with the same transcript, this may be evidence of this expression phenotype being a complex trait, affected by several genetic events. When the same set of loci commonly associate with a large number of transcripts, we have cross-confirmation of the individual associations as well as a possible multilocus effect on a pathway or a biological process.
GO and Pathway Analysis.
GO annotations for all transcripts were obtained by using publicly available Biomolecule Naming Service (http://openbns.sourceforge.net), a high-speed directory service that resolves between alias and official gene symbols and links to publicly available databases. We state that a transcript g is linked to a GO term t if t annotates g or is an ancestor of some GO annotation for g. For each GO term t and a list of transcripts L we test the hypothesis that the term t is overrepresented in L against the null hypothesis that distribution of terms is random. This term to transcript–list association is determined by using the hypergeometric distribution [for example, see Benjamini et al. (14)]. Namely, for each term t and list of transcripts L the P value is given by:
 |
where N equals the total number of unique GO annotated transcripts represented in the data set, n equals the total number of unique GO annotated transcripts represented in L, K equals the total number of transcripts linked to the GO term t, and k equals the number of entries in transcript list L linked to the GO term t.
A similar analysis was performed by using pathway information as follows. A pathway database containing 360 curated pathways from various sources such as Kyoto Encyclopedia of Genes and Genomes, BioCarta, and Signaling Pathway Database was used to search for overrepresentation of members of an expanded pathway. Overabundance was assessed by using the hypergeometric distribution similar to the algorithm described above.
Analysis of Correlations of Sets of Associated Transcripts.
The pair-wise correlations between expression of transcripts associated with SNPs in one gene was computed. For each set of SNPs in a gene we considered sets of transcripts associated with an SNP in this gene with P < 0.01. For each set of transcripts, we computed Pearson correlation between each pair of transcripts in the set, and we report the deviation of average correlation in the set from the expected expressed as the z score. We then compared the distribution of these z scores to the expected distribution, computed based on correlations in random sets of transcripts of the same size. The z score was computed as follows: Let Cij be the correlation of transcripts i and j from the set S. Let C0 be the average transcript-to-transcript correlation across the entire data set, and let σ0 be the corresponding standard deviation. For a set of transcripts S with n elements, there are N = n(n − 1)/2 transcript pairs. Then:
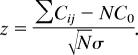 |
Assessment of Statistical Significance.
To assess the statistical significance of our findings, we used the FDR analysis to compare the results to those obtained on random data sets (19). Those were generated by randomly permuting the expression data while leaving the genotype data intact. This randomization process ensures that we keep the structure of dependencies between SNP loci that exist in the original data, as well as between expression vectors. These permuted data were used in assessing overabundance of significant SNP–transcript association pairs as well as in assessing the significance of more complex structures. We used 50 simulations to compute the ANOVA FDR. Genomic intervals on the chromosomes enriched for transcripts with a high average of statistically significant associations for each SNP were estimated as described by Lipson et al. (20).
Supplementary Material
Acknowledgments
This work was supported by Norwegian Cancer Society Grants D-99061 and D-03067, National Programme for Research in Functional Genomics Grant 152004/150, Norwegian Research Council Grant 155218/300, and a Swiss Bridge Award. R.S. was supported by an Alon fellowship. H.E. is a Fellow of the Norwegian Cancer Society.
Abbreviations
- SNP
single-nucleotide polymorphism
- ROS
reactive oxygen species
- GO
Gene Ontology
- FDR
false discovery rate
- QMIS
quantitative mutual information score
- LOOCV
leave-one-out cross-validation
- LD
linkage disequilibrium.
Footnotes
Conflict of interest statement: No conflicts declared.
References
- 1.Morley M., Molony C. M., Weber T. M., Devlin J. L., Ewens K. G., Spielman R. S., Cheung V. G. Nature. 2004;430:743–747. doi: 10.1038/nature02797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Bystrykh L., Weersing E., Dontje B., Sutton S., Pletcher M. T., Wiltshire T., Su A. I., Vellenga E., Wang J., Manly K. F., et al. Nat. Genet. 2005;37:225–232. doi: 10.1038/ng1497. [DOI] [PubMed] [Google Scholar]
- 3.Chesler E. J., Lu L., Shou S., Qu Y., Gu J., Wang J., Hsu H. C., Mountz J. D., Baldwin N. E., Langston M. A., et al. Nat. Genet. 2005;37:233–242. doi: 10.1038/ng1518. [DOI] [PubMed] [Google Scholar]
- 4.Hubner N., Wallace C. A., Zimdahl H., Petretto E., Schulz H., Maciver F., Mueller M., Hummel O., Monti J., Zidek V., et al. Nat. Genet. 2005;37:243–253. doi: 10.1038/ng1522. [DOI] [PubMed] [Google Scholar]
- 5.Pastinen T., Sladek R., Gurd S., Sammak A., Ge B., Lepage P., Lavergne K., Villeneuve A., Gaudin T., Brandstrom H., et al. Physiol. Genomics. 2004;16:184–193. doi: 10.1152/physiolgenomics.00163.2003. [DOI] [PubMed] [Google Scholar]
- 6.Perou C. M., Sorlie T., Eisen M. B., van de Rijn M., Jeffrey S. S., Rees C. A., Pollack J. R., Ross D. T., Johnsen H., Akslen L. A., et al. Nature. 2000;406:747–752. doi: 10.1038/35021093. [DOI] [PubMed] [Google Scholar]
- 7.Sorlie T., Perou C. M., Tibshirani R., Aas T., Geisler S., Johnsen H., Hastie T., Eisen M. B., van de Rijn M., Jeffrey S. S., et al. Proc. Natl. Acad. Sci. USA. 2001;98:10869–10874. doi: 10.1073/pnas.191367098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sorlie T., Tibshirani R., Parker J., Hastie T., Marron J. S., Nobel A., Deng S., Johnsen H., Pesich R., Geisler S., et al. Proc. Natl. Acad. Sci. USA. 2003;100:8418–8423. doi: 10.1073/pnas.0932692100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Edvardsen H., Irene Grenaker A. G., Tsalenko A., Mulcahy T., Yuryev A., Lindersson M., Lien S., Omholt S., Syvanen A. C., Borresen-Dale A. L., et al. Pharmacogenet. Genomics. 2006;16:207–217. doi: 10.1097/01.fpc.0000194422.12770.fb. [DOI] [PubMed] [Google Scholar]
- 10.Rice J. A. Mathematical Statistics and Data Analysis. 2nd Ed. Belmont, CA: Thomson Higher Education; 1995. [Google Scholar]
- 11.Tsalenko A., Ben-Dor A., Cox N., Yakhini Z. Pac. Symp. Biocomput. 2003:548–561. doi: 10.1142/9789812776303_0051. [DOI] [PubMed] [Google Scholar]
- 12.Hedenfalk I., Ringner M., Ben-Dor A., Yakhini Z., Chen Y., Chebil G., Ach R., Loman N., Olsson H., Meltzer P., et al. Proc. Natl. Acad. Sci. USA. 2003;100:2532–2537. doi: 10.1073/pnas.0533805100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Tanay A., Sharan R., Kupiec M., Shamir R. Proc. Natl. Acad. Sci. USA. 2004;101:2981–2986. doi: 10.1073/pnas.0308661100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Benjamini Y., Hochberg Y. J. R. Stat. Soc. B. 1995;57:289–300. [Google Scholar]
- 15.Tsalenko A., Sharan R., Edvardsen H., Kristensen V. N., Borresen-Dale A. L., Ben-Dor A., Yakhini Z. J. BioComput. Bioinformatics. 2006 doi: 10.1142/s0219720006001953. in press. [DOI] [PubMed] [Google Scholar]
- 16.Spilianakis C. G., Lalioti M. D., Town T., Lee G. R., Flavell R. A. Nature. 2005;435:637–645. doi: 10.1038/nature03574. [DOI] [PubMed] [Google Scholar]
- 17.van’t Veer L. J., Dai H., van de Vijver M. J., He Y. D., Hart A. A., Mao M., Peterse H. L., van der Kooy K., Marton M. J., Witteveen A. T., et al. Nature. 2002;415:530–536. doi: 10.1038/415530a. [DOI] [PubMed] [Google Scholar]
- 18.Barrett J. C., Fry B., Maller J., Daly M. J. Bioinformatics. 2005;21:263–265. doi: 10.1093/bioinformatics/bth457. [DOI] [PubMed] [Google Scholar]
- 19.Draghici S., Khatri P., Bhavsar P., Shah A., Krawetz S. A., Tainsky M. A. Nucleic Acids Res. 2003;31:3775–3781. doi: 10.1093/nar/gkg624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lipson D., Aumann Y., Ben-Dor A., Linial N., Yakhini Z. Proceedings of RECOMB 2005, LNCS; Berlin: Springer; 2005. pp. 83–94. [Google Scholar]
- 21.Tsalenko A., Sharon R., Edvardsen H., Kristensen V., Børresen-Dale A.-L., Ben-Dor A., Yakhini Z. Proc. IEEE Comput. Syst. Bioinform. Conference; 2005. pp. 135–143. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.